题目内容
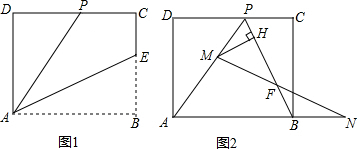
16.已知矩形ABCD的一条边AD=8,E是BC边上的一点,将矩形ABCD沿折痕AE折叠,使得顶点B落在CD边上的点P处,PC=4(如图1).(1)求AB的长;
(2)擦去折痕AE,连结PB,设M是线段PA的一个动点(点M与点P、A不重合).N是AB沿长线上的一个动点,并且满足PM=BN.过点M作MH⊥PB,垂足为H,连结MN交PB于点F(如图2).
①若M是PA的中点,求MH的长;
②试问当点M、N在移动过程中,线段FH的长度是否发生变化?若变化,说明理由;若不变,求出线段FH的长度.
分析 (1)设AB=x,根据折叠可得AP=CD=x,DP=CD-CP=x-4,利用勾股定理,在Rt△ADP中,AD2+DP2=AP2,即82+(x-4)2=x2,即可解答;
(2)①过点A作AG⊥PB于点G,根据勾股定理求出PB的长,由AP=AB,所以PG=BG=$\frac{1}{2}$PB=2$\sqrt{5}$,在Rt△AGP中,AG=$\sqrt{A{P}^{2}-P{G}^{2}}=\sqrt{1{0}^{2}-(2\sqrt{5})^{2}}=4\sqrt{5}$,
由AG⊥PB,MH⊥PB,所以MH∥AG,根据M是PA的中点,所以H是PG的中点,根据中位线的性质得到MH=$\frac{1}{2}$AG=$\frac{1}{2}×4\sqrt{5}=2\sqrt{5}$.
②作MQ∥AN,交PB于点Q,求出MP=MQ,BN=QM,得出MP=MQ,根据MH⊥PQ,得出HQ=$\frac{1}{2}$PQ,根据∠QMF=∠BNF,证出△MFQ≌△NFB,得出QF=$\frac{1}{2}$QB,再求出EF=$\frac{1}{2}$PB,最后代入HF=$\frac{1}{2}$PB即可得出线段EF的长度不变.
解答 解:(1)设AB=x,则AP=CD=x,DP=CD-CP=x-4,
在Rt△ADP中,AD2+DP2=AP2,
即82+(x-4)2=x2,
解得:x=10,
即AB=10.
(2)①如图2,过点A作AG⊥PB于点G,
由(1)中的结论可得:PC=4,BC=8,∠C=90°,
∴PB=$\sqrt{B{C}^{2}+P{C}^{2}}=\sqrt{{8}^{2}+{4}^{2}}=4\sqrt{5}$,
∵AP=AB,
∴PG=BG=$\frac{1}{2}$PB=2$\sqrt{5}$,
在Rt△AGP中,AG=$\sqrt{A{P}^{2}-P{G}^{2}}=\sqrt{1{0}^{2}-(2\sqrt{5})^{2}}=4\sqrt{5}$,
∵AG⊥PB,MH⊥PB,
∴MH∥AG,
∵M是PA的中点,
∴H是PG的中点,
∴MH=$\frac{1}{2}$AG=$\frac{1}{2}×4\sqrt{5}=2\sqrt{5}$.
②当点M、N在移动过程中,线段FH的长度是不发生变化;
作MQ∥AN,交PB于点Q,如图3,
∵AP=AB,MQ∥AN,
∴∠APB=∠ABP=∠MQP.
∴MP=MQ,
∵BN=PM,
∴BN=QM.
∵MP=MQ,MH⊥PQ,
∴HQ=$\frac{1}{2}$PQ.
∵MQ∥AN,
∴∠QMF=∠BNF,
在△MFQ和△NFB中,
$\left\{\begin{array}{l}{∠QFM=∠NFB}\\{∠QMF=∠BNF}\\{MQ=BN}\end{array}\right.$,
∴△MFQ≌△NFB(AAS).
∴QF=$\frac{1}{2}$QB,
∴HF=HQ+QF=$\frac{1}{2}$PQ+$\frac{1}{2}$QB=$\frac{1}{2}$PB=$\frac{1}{2}×4\sqrt{5}=2\sqrt{5}$.
∴当点M、N在移动过程中,线段FH的长度是不发生变化,长度为2$\sqrt{5}$.
点评 此题考查了四边形综合,用到的知识点是全等三角形的判定与性质、勾股定理、等腰三角形的性质,关键是做出辅助线,找出全等三角形.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | ±1 | B. | 0 | C. | 1 | D. | -1 |
 如图,若l1∥l2,∠1=x°,则∠2=(180-x)°.
如图,若l1∥l2,∠1=x°,则∠2=(180-x)°.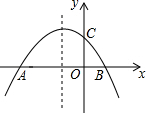 已知二次函数y=-x2-x+2的图象与x轴分别交于A、B两点(如图所示),与y轴交于点C,点P是其对称轴上一动点,当PB+PC取得最小值时,点P的坐标为(-$\frac{1}{2}$,$\frac{3}{2}$).
已知二次函数y=-x2-x+2的图象与x轴分别交于A、B两点(如图所示),与y轴交于点C,点P是其对称轴上一动点,当PB+PC取得最小值时,点P的坐标为(-$\frac{1}{2}$,$\frac{3}{2}$).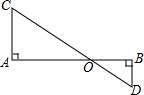 如图,AB与CD交于O点,已知AC⊥AB,BD⊥AB,AO=50cm,BO=25cm,CD=150cm,求CO和DO.
如图,AB与CD交于O点,已知AC⊥AB,BD⊥AB,AO=50cm,BO=25cm,CD=150cm,求CO和DO. 如图,Rt△ABC中,∠A=90°,AD⊥BC于点D,若BD:CD=3:2,则tanB=$\frac{\sqrt{6}}{3}$.
如图,Rt△ABC中,∠A=90°,AD⊥BC于点D,若BD:CD=3:2,则tanB=$\frac{\sqrt{6}}{3}$.