题目内容
16.便民商店经营一种商品,在销售过程中,发现一周利润y(元)与每件销售价x(元)之间的关系满足y=-2x2+80x+750,由于某种原因,售价只能满足25≤x≤30,那么一周可获得的最大利润是1550元.分析 先将求二次函数变形为y=-2(x-20)2+1550,根据顶点式在15≤x≤22范围内求函数的最大值,因为该二次函数的开口方向向下,所以当x-20=0时,y取最大值1550,故得出结论.
解答 解:∵y=-2x2+80x+750,
∴y=-2(x-20)2+1550,
∵a=-2<0,抛物线开口向下,函数有最大值,
∴x=20时,y最大=1550.
∵x=20在25≤x≤30范围内,
∴y的最大值为1550.
故答案为:1550.
点评 本题考查了二次函数的应用.求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法.此题要注意x的取值范围,在15≤x≤22范围内求解.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
11.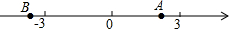 点A,B在数轴上的位置如图所示,其对应的数分别是a和b,对于以下结论:甲:b-a<0;乙:a+b>0;丙:|a|<|b|;丁:ab>0,其中正确的是( )
点A,B在数轴上的位置如图所示,其对应的数分别是a和b,对于以下结论:甲:b-a<0;乙:a+b>0;丙:|a|<|b|;丁:ab>0,其中正确的是( )
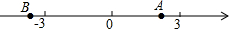 点A,B在数轴上的位置如图所示,其对应的数分别是a和b,对于以下结论:甲:b-a<0;乙:a+b>0;丙:|a|<|b|;丁:ab>0,其中正确的是( )
点A,B在数轴上的位置如图所示,其对应的数分别是a和b,对于以下结论:甲:b-a<0;乙:a+b>0;丙:|a|<|b|;丁:ab>0,其中正确的是( )| A. | 甲、乙 | B. | 丙、丁 | C. | 甲、丙 | D. | 乙、丁 |
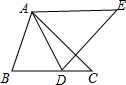 如图,AB=AD,BC=DE,∠BAD=∠CDE.
如图,AB=AD,BC=DE,∠BAD=∠CDE. 请分析如图图案的形成过程.
请分析如图图案的形成过程. 如图两幅图案是怎样利用旋转、平移或对称进行设计的?
如图两幅图案是怎样利用旋转、平移或对称进行设计的?