题目内容
6.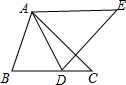 如图,AB=AD,BC=DE,∠BAD=∠CDE.
如图,AB=AD,BC=DE,∠BAD=∠CDE.求证:(1)AC=AE;(2)∠CAE=∠CDE.
分析 (1)根据外角的性质结合∠BAD=∠CDE即可得出∠B=∠ADE,再根据AB=AD、BC=DE即可证出△ABC≌△ADE(SAS),进而得出AC=AE;
(2)根据△ABC≌△ADE即可得出∠BAC=∠DAE,通过角的计算即可得出∠BAD=∠CAE,再结合∠BAD=∠CDE即可证出∠CAE=∠CDE.
解答 证明:(1)∵∠ADC=∠ADE+∠EDC=∠B+∠BAD,且∠BAD=∠CDE,
∴∠B=∠ADE.
在△ABC和△ADE中,$\left\{\begin{array}{l}{AB=AD}\\{∠B=∠ADE}\\{BC=DE}\end{array}\right.$,
∴△ABC≌△ADE(SAS),
∴AC=AE.
(2)∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE.
∵∠BAD=∠CDE,
∴∠CAE=∠CDE.
点评 本题考查了全等三角形的判定与性质以及三角形外角的性质,熟练掌握各全等三角形的判定定理是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.下列各式中,等号不成立的是( )
| A. | |-3|=3 | B. | -|3|=-|-3| | C. | |3|=|-3| | D. | -|-3|=3 |
11.下列实数-$\sqrt{2}$,$\frac{π}{2}$,$\frac{22}{7}$,0.1414,$\root{3}{9}$,$\sqrt{11}$,0.2002000200002中,无理数的个数是( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
18.已知p与q互为相反数,且p≠0,那么下列关系式正确的是( )
| A. | p•q=1 | B. | p+q=0 | C. | p+q=1 | D. | p-q=0 |