题目内容
 如图,在平面直角坐标系中,点A的坐标为(-1,0),点B的坐标为(0,2),以点A为中心,将线段AB逆时针旋转90°,则点B的对应点B′的坐标是
如图,在平面直角坐标系中,点A的坐标为(-1,0),点B的坐标为(0,2),以点A为中心,将线段AB逆时针旋转90°,则点B的对应点B′的坐标是考点:坐标与图形变化-旋转
专题:
分析:过点B′作B′C⊥x轴于C,根据点A、B的坐标求出OA、OB的长,再根据旋转的性质和等角的余角相等求出∠B′AC=∠ABO,然后利用“角角边”证明△ABO和△B′AC全等,根据全等三角形对应边相等可得B′C=OA,AC=OB,再求出OC,然后写出点B′的坐标即可.
解答: 解:如图,过点B′作B′C⊥x轴于C,
解:如图,过点B′作B′C⊥x轴于C,
∵A(-1,0),B(0,2),
∴OA=1,OB=2,
∵线段AB逆时针旋转90°得到AB′,
∴∠BAB′=90°,AB=AB′,
∴∠B′AC+∠BAO=90°,
又∵∠ABO+∠BAO=90°,
∴∠B′AC=∠ABO,
在△ABO和△B′AC中,
,
∴△ABO≌△B′AC(AAS),
∴B′C=OA=1,AC=OB=2,
∴OC=OA+AC=1+2=3,
∴点B′的坐标是(-3,1).
故答案为:(-3,1).
 解:如图,过点B′作B′C⊥x轴于C,
解:如图,过点B′作B′C⊥x轴于C,∵A(-1,0),B(0,2),
∴OA=1,OB=2,
∵线段AB逆时针旋转90°得到AB′,
∴∠BAB′=90°,AB=AB′,
∴∠B′AC+∠BAO=90°,
又∵∠ABO+∠BAO=90°,
∴∠B′AC=∠ABO,
在△ABO和△B′AC中,
|
∴△ABO≌△B′AC(AAS),
∴B′C=OA=1,AC=OB=2,
∴OC=OA+AC=1+2=3,
∴点B′的坐标是(-3,1).
故答案为:(-3,1).
点评:本题考查了坐标与图形变化-旋转,熟记旋转变换只改变图形的位置不改变图形的形状与大小得到相等边是解题的关键,作出图形更形象直观.

练习册系列答案
相关题目
 如图,在△ABC中,∠A=72°,AB=AC,BD平分∠ABC,且BD=BE,点D、E分别在AC、BC上,则∠DEB=( )
如图,在△ABC中,∠A=72°,AB=AC,BD平分∠ABC,且BD=BE,点D、E分别在AC、BC上,则∠DEB=( )| A、76° | B、75.5° |
| C、76.5° | D、75° |
若两个不相等的实数m、n满足m2-6m=4,n2-4=6n,则mn的值为( )
| A、6 | B、-6 | C、4 | D、-4 |
化简
-a
得( )
| -a3 |
-
|
A、(a-1)
| ||
B、(1-a)
| ||
C、-(a+1)
| ||
D、(a-1)
|
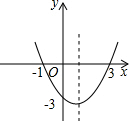 已知二次函数的图象如图,则这个二次函数的表达式为
已知二次函数的图象如图,则这个二次函数的表达式为