题目内容
14．如果连续抛掷3枚普通硬币．（1）利用树状图或列表法写出所有机会均等的结果；
（2）求出第1、2两枚“出现正面”的概率．
分析 （1）首先根据题意画出树状图，然后由树状图求得所有等可能的结果；
（2）由树状图即可得第1、2两枚“出现正面”的有6种情况，然后直接利用概率公式求解即可求得答案．
解答 解：（1）画树状图得：
则共有8种等可能的结果；
（2）∵第1、2两枚“出现正面”的有6种情况，
∴第1、2两枚“出现正面”的概率为：$\frac{6}{8}$=$\frac{3}{4}$．
点评 此题考查了树状图法与列表法求概率．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
5．
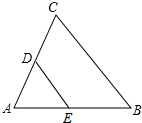如图，在△ABC中，D、E分别是边AC、AB上的点，下列命题中，假命题是（ ）
如图，在△ABC中，D、E分别是边AC、AB上的点，下列命题中，假命题是（ ）| A． | 若$\frac{AD}{AC}$=$\frac{DE}{BC}$，则△ADE与△ABC相似 | B． | 若$\frac{AD}{DC}$=$\frac{AE}{EB}$，则△ADE与△ABC相似 | ||
| C． | 若$\frac{AD}{AB}$=$\frac{AE}{AC}$，则△ADE与△ABC相似 | D． | 若∠ADE=∠B，则△ADE与△ABC相似 |
3．
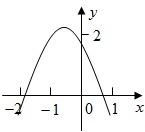如图，二次函数y=ax2+bx+c（a≠0）的图象经过点（-1，2），且与X轴交点的横坐标分别为x1，x2，其中-2＜x1＜-1，0＜x2＜1，下列结论：
①4a-2b+c＜0；②2a-b＜0；③a+c＜1；④b2+8a＞4ac，
其中正确的有（ ）
如图，二次函数y=ax2+bx+c（a≠0）的图象经过点（-1，2），且与X轴交点的横坐标分别为x1，x2，其中-2＜x1＜-1，0＜x2＜1，下列结论：①4a-2b+c＜0；②2a-b＜0；③a+c＜1；④b2+8a＞4ac，
其中正确的有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
4．下列运算中，结果正确的是（ ）
| A． | x3+x2=x5 | B． | （x2）3=x6 | C． | x3•x2=x6 | D． | （x+y）2=x2+y2 |