题目内容
9.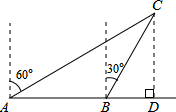 如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进40海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海岛C到航线AB的距离CD是( )
如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进40海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海岛C到航线AB的距离CD是( )| A. | 20海里 | B. | 40海里 | C. | 20$\sqrt{3}$海里 | D. | 40$\sqrt{3}$海里 |
分析 根据方向角的定义及余角的性质求出∠CAD=30°,∠CBD=60°,再由三角形外角的性质得到∠CAD=30°=∠ACB,根据等角对等边得出AB=BC=20,然后解Rt△BCD,求出CD即可解答.
解答 解:根据题意可知∠CAD=30°,∠CBD=60°,
∵∠CBD=∠CAD+∠ACB,
∴∠CAD=30°=∠ACB,
∴AB=BC=40海里,
在Rt△CBD中,∠BDC=90°,∠DBC=60°,sin∠DBC=$\frac{CD}{BC}$,
∴sin60°=$\frac{CD}{BC}$,
∴CD=40×sin60°=40×$\frac{\sqrt{3}}{2}$=20$\sqrt{3}$(海里).
故选:C.
点评 本题考查了解直角三角形的应用,难度适中.解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
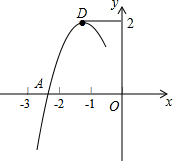 抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:
抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论: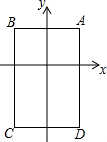 在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2),把一条长为2016个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D-A-….的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是(0,-2).
在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2),把一条长为2016个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D-A-….的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是(0,-2).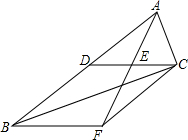 如图,CD是△ABC的中线,点E是AF的中点,CF∥AB.
如图,CD是△ABC的中线,点E是AF的中点,CF∥AB.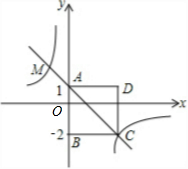 如图,四边形ABCD为正方形,点A的坐标为(0,1),点B的坐标为(0,-2),反比例函数y=$\frac{k}{x}$的图象经过点C,一次函数y=ax+b的图象经过A、C两点
如图,四边形ABCD为正方形,点A的坐标为(0,1),点B的坐标为(0,-2),反比例函数y=$\frac{k}{x}$的图象经过点C,一次函数y=ax+b的图象经过A、C两点
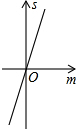
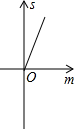
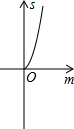
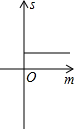
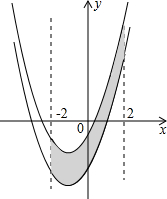 如图,已知抛物线y=x2+2x-3,把此抛物线沿y轴向上平移,平移后的抛物线和原抛物线及直线x=2,x=-2所围成的阴影部分的面积为S,平移的距离为m,则下列图象中,能表示S与m的函数关系的图象大致是( )
如图,已知抛物线y=x2+2x-3,把此抛物线沿y轴向上平移,平移后的抛物线和原抛物线及直线x=2,x=-2所围成的阴影部分的面积为S,平移的距离为m,则下列图象中,能表示S与m的函数关系的图象大致是( )