题目内容
△ABC中,O为BC上一点,⊙O过A、C两点交BC于D,BA为⊙O的切线.
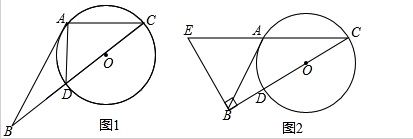
(1)如图1,若AD=1,AC=2,求tan∠BAD的值;
(2)如图2,过B作BE⊥BC交CA的延长线于E,若AC:AE=2:3,求tan∠ABD的值.

(1)如图1,若AD=1,AC=2,求tan∠BAD的值;
(2)如图2,过B作BE⊥BC交CA的延长线于E,若AC:AE=2:3,求tan∠ABD的值.
考点:切线的性质,解直角三角形
专题:计算题
分析:(1)连结OA,如图1,根据切线的性质得∠OAB=90°,即∠BAD+∠OAD=90°,再根据圆周角定理,由CD为直径得到∠CAO+∠OAD=90°,则∠BAD=∠CAO,加上∠CAO=∠ACO,所以∠BAD=∠ACO,在Rt△ADC中利用勾股定理计算出CD=
,然后根据正切的定义求解;
(2)作BF⊥AE于F,连结OA、AD,如图2,设⊙O的半径为r,先根据等角的余角相等得到∠E=∠BAE,而BF⊥AE,根据等腰三角形的性质得AF=EF,由AC:AE=2:3得到AC:AF=4:3,再证明AD∥AC,利用比例线段得到BD=
r,则OB=
r,在Rt△ABO中,利用勾股定理得AB=
r,然后根据正切的定义求解.
| 5 |
(2)作BF⊥AE于F,连结OA、AD,如图2,设⊙O的半径为r,先根据等角的余角相等得到∠E=∠BAE,而BF⊥AE,根据等腰三角形的性质得AF=EF,由AC:AE=2:3得到AC:AF=4:3,再证明AD∥AC,利用比例线段得到BD=
| 3 |
| 2 |
| 5 |
| 2 |
| ||
| 2 |
解答:解:(1)连结OA,如图1,
∵BA为⊙O的切线,
∴OA⊥AB,
∴∠OAB=90°,即∠BAD+∠OAD=90°,
∵CD为直径,
∴∠CAD=90°,即∠CAO+∠OAD=90°,
∴∠BAD=∠CAO,
∵OA=OC,
∴∠CAO=∠ACO,
∴∠BAD=∠ACO,
在Rt△ADC中,∵AD=1,AC=2,
∴CD=
=
,
∴tan∠ACD=
=
=
,
∴tan∠BAD=
;
(2)作BF⊥AE于F,连结OA、AD,如图2,设⊙O的半径为r,
∵BA为⊙O的切线,
∴OA⊥AB,
∴∠OAB=90°,
∴∠BAE+∠OAC=90°,
而∠CAO=∠ACO,
∴∠BAE+∠ACO=90°,
∵BE⊥BC,
∴∠E+∠BCE=90°,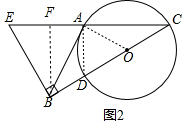
∴∠E=∠BAE,
而BF⊥AE,
∴AF=EF,
∵AC:AE=2:3,
∴AC:AF=4:3,
∵∠DAC=90°,
∴AD∥AC
∴
=
,即
=
,
∴BD=
r
∴OB=r+
r=
r,
在RT△ABO中,AB=
=
r,
∴tan∠ABO=
=
,
即tan∠ABD的值为
.

∵BA为⊙O的切线,
∴OA⊥AB,
∴∠OAB=90°,即∠BAD+∠OAD=90°,
∵CD为直径,
∴∠CAD=90°,即∠CAO+∠OAD=90°,
∴∠BAD=∠CAO,
∵OA=OC,
∴∠CAO=∠ACO,
∴∠BAD=∠ACO,
在Rt△ADC中,∵AD=1,AC=2,
∴CD=
| AD2+AC2 |
| 5 |
∴tan∠ACD=
| AD |
| CD |
| 1 | ||
|
| ||
| 5 |
∴tan∠BAD=
| ||
| 5 |
(2)作BF⊥AE于F,连结OA、AD,如图2,设⊙O的半径为r,
∵BA为⊙O的切线,
∴OA⊥AB,
∴∠OAB=90°,
∴∠BAE+∠OAC=90°,
而∠CAO=∠ACO,
∴∠BAE+∠ACO=90°,
∵BE⊥BC,
∴∠E+∠BCE=90°,

∴∠E=∠BAE,
而BF⊥AE,
∴AF=EF,
∵AC:AE=2:3,
∴AC:AF=4:3,
∵∠DAC=90°,
∴AD∥AC
∴
| CD |
| BD |
| CA |
| AF |
| 2r |
| BD |
| 4 |
| 3 |
∴BD=
| 3 |
| 2 |
∴OB=r+
| 3 |
| 2 |
| 5 |
| 2 |
在RT△ABO中,AB=
| OB2-OA2 |
| ||
| 2 |
∴tan∠ABO=
| OA |
| AB |
2
| ||
| 21 |
即tan∠ABD的值为
2
| ||
| 21 |
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了平行线分线段成比例定理和锐角三角函数.

练习册系列答案
相关题目
在△ABC中,O为内心,∠A=80°,则∠BOC=( )
| A、140° | B、135° |
| C、130° | D、125° |
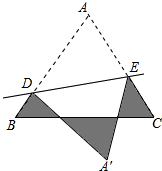 如图,等边三角形ABC的边长为1cm,DE分别是AB、AC上的点,将△ABC沿直线DE折叠,点A落在点A′处,且点A′在△ABC外部,则阴影部分的周长为( )
如图,等边三角形ABC的边长为1cm,DE分别是AB、AC上的点,将△ABC沿直线DE折叠,点A落在点A′处,且点A′在△ABC外部,则阴影部分的周长为( )| A、2cm | B、2.5cm |
| C、3cm | D、3.5cm |
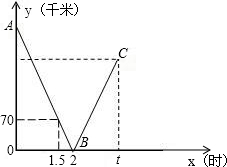 一辆快车和一辆慢车分别从甲、乙两地出发,匀速相向而行,相遇后继续前行,已知两车相遇时快车比慢车多行驶40千米,设行驶的路程为x(小时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.
一辆快车和一辆慢车分别从甲、乙两地出发,匀速相向而行,相遇后继续前行,已知两车相遇时快车比慢车多行驶40千米,设行驶的路程为x(小时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.