题目内容
17．
《九章算术》是中国传统数学最重要的著作，奠定了中国传统数学的基本框架．其中卷第九勾股，主要讲述了以测量问题为中心的直角三角形三边互求的关系．其中记载：“今有邑方二百步，各中开门．出东门一五步有木．问出南门几何步而见木？”译文：“今有正方形小城边长为200步，各方中央开一城门．走出东门15步处有树，问出南门多少步能见到树？”请你结合题意画出图形，并完成求解．
分析 根据题意写出AB、AC、CD的长，根据相似三角形的性质得到比例式，计算即可．
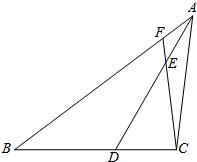
解答 解：如图所示：
由题意得，AB=15步，AC=100步，CD=100步，
△ACB∽△DEC，
则$\frac{DE}{AC}=\frac{CD}{AB}$，即$\frac{DE}{100}=\frac{100}{15}$，
解得DE=$\frac{2000}{3}$．
故走出南门$\frac{2000}{3}$步恰好能见到这棵树．
点评 本题考查的是直角三角形三边关系、相似三角形的判定与性质；掌握相似三角形的判定定理和性质定理是解题的关键．
练习册系列答案
培优口算题卡系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
8．下列运算中，错误的是（ ）
| A． | $\frac{1}{4}$÷（-4）=4×（-4） | B． | -5÷（-$\frac{1}{2}$）=-5×（-2） | C． | 7-（-3）=7+3 | D． | 6-7=（+6）+（-7） |
已知：如图，△ABC中，AD平分∠BAC交BC于点D，且∠ADC=60°，若∠ACB为钝角，且AB＞AC，BD＞DC．
如图，在⊙O中，弦AB垂直平分半径OC．
9．
有这样一个问题：探究函数y=$\frac{1}{{{x^2}-1}}$的图象与性质．
小东根据学习函数的经验，对函数y=$\frac{1}{{{x^2}-1}}$的图象与性质进行了探究．下面是小东的探究过程，请补充完成：
（1）自变量取值范围：x≠±1
（2）画图象
①列表
②描点：（见坐标系）
③连线：请你在坐标系中补全图象
（3）进一步探究发现，该函数图象在y轴上有一交点为（0，-1），结合图象，请你写出该函数的其他性质
（一条即可）：x＜-1时y随x增大而增大．
有这样一个问题：探究函数y=$\frac{1}{{{x^2}-1}}$的图象与性质．小东根据学习函数的经验，对函数y=$\frac{1}{{{x^2}-1}}$的图象与性质进行了探究．下面是小东的探究过程，请补充完成：
（1）自变量取值范围：x≠±1
（2）画图象
①列表
| x | … | -$\frac{9}{4}$ | -2 | -$\frac{7}{4}$ | -$\frac{3}{2}$ | -$\frac{5}{4}$ | … |
| y | … | 0.25 | 0.33 | 0.48 | 0.8 | 1.78 | … |
| x | -$\frac{3}{4}$ | -$\frac{1}{2}$ | $\frac{1}{4}$ | 0 | $\frac{1}{4}$ | $\frac{1}{2}$ | $\frac{3}{4}$ |
| y | -2.29 | -1.33 | -1.07 | -1 | -1.07 | -1.33 | -2.29 |
| x | … | $\frac{5}{4}$ | $\frac{3}{2}$ | $\frac{7}{4}$ | 2 | $\frac{9}{4}$ | … |
| y | … | 1.78 | 0.8 | 0.48 | 0.33 | 0.25 | … |
③连线：请你在坐标系中补全图象
（3）进一步探究发现，该函数图象在y轴上有一交点为（0，-1），结合图象，请你写出该函数的其他性质
（一条即可）：x＜-1时y随x增大而增大．
如图，正方形ABCD，顶点B在直线MN上，AE⊥MN，CF⊥MN，垂足分别为E、F且AE=1，CF=2．求正方形ABCD的面积．