题目内容
10.(1)计算:$-{3^2}+|{-\sqrt{2}-3}|{({π-2})^0}-\sqrt{8}+{({-\frac{1}{3}})^{-1}}$(2)解方程:x2-6x-2=0.
分析 (1)原式第一项利用乘方的意义化简,第二项利用绝对值的代数意义化简,第三项化为最简二次根式,最后一项利用负整数指数幂法则计算即可得到结果;
(2)方程整理后,利用配方法求出解即可.
解答 解:(1)原式=-9+$\sqrt{2}$+3-2$\sqrt{2}$-3=-9-$\sqrt{2}$;
(2)方程变形得:x2-6x=2,
配方得:x2-6x+9=11,即(x-3)2=11,
开方得:x-3=±$\sqrt{11}$,
解得:x1=3+$\sqrt{11}$,x2=3-$\sqrt{11}$.
点评 此题考查了实数的运算,以及解一元二次方程-配方法,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
20.已知:x1,x2是一元二次方程x2+2ax+b=0的两根,且x1+x2=4,x1x2=1,则a,b的值分别是( )
| A. | a=-4,b=1 | B. | a=4,b=1 | C. | a=-2,b=1 | D. | a=-2,b=-1 |
1.在函数y=$\frac{12}{x}$图象上的点是( )
| A. | (-2,6) | B. | (-2,-6) | C. | (3,-4) | D. | (-3,4) |
2.一家鞋店在一段时间内销售了某种男鞋200双,各种尺码鞋的销售量如表所示:
一般来讲鞋店老板比较关心哪种尺码的鞋最畅销,也就是关心卖出的鞋的尺码组成的一组数据( )
| 尺码/厘米 | 23 | 23.5 | 24 | 24.5 | 25 | 25.5 |
| 销售量/双 | 5 | 10 | 22 | 39 | 56 | 43 |
| A. | 平均数 | B. | 中位数 | C. | 众数 | D. | 加权平均数 |
 方格纸中每个小方格都是边长为1个单位长度的正方形,在平面直角坐标系中,已知点A(3,4)、B(-4,3)、C(3,-2).
方格纸中每个小方格都是边长为1个单位长度的正方形,在平面直角坐标系中,已知点A(3,4)、B(-4,3)、C(3,-2).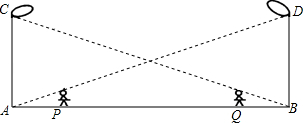 如图所示,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶点刚好接触到路灯AC的底部,当他向前再走行20m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学身高是1.5m,两个路灯的高度都是9m,则两路灯之间的距离是多少?
如图所示,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶点刚好接触到路灯AC的底部,当他向前再走行20m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学身高是1.5m,两个路灯的高度都是9m,则两路灯之间的距离是多少?