题目内容

7．若直线y=ax+b与x轴的交点到y轴的距离为1，则关于x的一元一次方程ax+b=0的解为±1．

分析 根据直线与x轴的交点的求法得出交点坐标（-$\frac{b}{a}$，0），根据题意得出-$\frac{b}{a}$=±1，从而得出答案．

解答 解：∵直线与x轴的交点的求法得出交点坐标（-$\frac{b}{a}$，0），且交点到y轴的距离为1，
∴-$\frac{b}{a}$=±1
∴关于x的一元一次方程ax+b=0的解为x=±1，
故答案为±1．

点评 本题考查了一次函数与一元一次方程的关系，掌握一次函数的性质是解题的关键．

练习册系列答案
相关题目
15．端午节“赛龙舟，吃粽子”是中华民族的传统习俗．节日期间，小邱家包了三种不同馅的粽子，分别是：红枣粽子（记为A），豆沙粽子（记为B），肉粽子（记为C），这些粽子除了馅不同，其余均相同．粽子煮好后，小邱的妈妈给一个白盘中放入了两个红枣粽子，一个豆沙粽子和一个肉粽子；给一个花盘中放入了两个肉粽子，一个红枣粽子和一个豆沙粽子．
根据以上情况，请你回答下列问题：
（1）假设小邱从白盘中随机取一个粽子，恰好取到红枣粽子的概率是多少？
（2）若小邱先从白盘里的四个粽子中随机取一个粽子，再从花盘里的四个粽子中随机取一个粽子，请用列表法或画树状图的方法，求小邱取到的两个粽子中一个是红枣粽子、一个是豆沙粽子的概率．
18．如图，在△ABC中，M、N分别为BC、AC上一点，AM和BN都交于点D，BM=tMC，点D为AM的中点．

（1）当t=1时，求$\frac{BD}{BN}$的值；
（2）当t=3时，求$\frac{AN}{AC}$的值；
（3）若S△BDM=2S△DNC，求t的值．
15．已知抛物线L：y=ax2+bx+c与抛物线L′：y=x2-2mx+4m+1关于直线x=2对称，且L′交y轴于点P（0，21），则方程ax2+bx+c=0的两个根为（　　）
A．x1=0，x2=3B．x1=1，x2=-3C．x1=3，x2=7D．x1=-7，x2=-3
2．图甲、图乙是两张形状、大小完全相同的6×6方格纸，方格纸中的每个小正方形的边长均为1，点A，B在小正方形的顶点上．

（1）在图甲中画出一个以点A，B为顶点的平行四边形（要求所作的平行四边形不是菱形且各顶点都在格点上），并求出它的周长．
（2）在图乙中画出一个以点A，B为顶点的菱形（要求所作的菱形各顶点都在格点上），并求出它的面积．
（注：图甲、图乙在答题纸上）
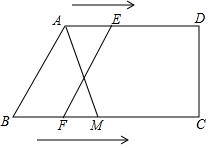12．在四边形ABCD中，AD∥BC，BC⊥CD，AD=6cm，BC=10cm，点E从A出发以1cm/s的速度向D运动，点F从点B出发，以2cm/s的速度向点C运动，当其中一点到达终点，而另一点也随之停止，设运动时间为t，
（1）t取何值时，四边形EFCD为矩形？
（2）M是BC上一点，且BM=4，t取何值时，以A、M、E、F为顶点的四边形是平行四边形？
19．已知双曲线y=$\frac{k}{x}$经过点（m，n），（n+1，m-1），（m2-1，n2-1），则k的值为（　　）
A．0或3B．0或-3C．-3D．3
16．如图，在方格纸中，每个小正方形边长都是1，?ABCD的四个顶点都在小方格的顶点上，按下列要求画一个面积与?ABCD面积相等的四边形，使它的顶点均在方格的顶点上．（四边形的边用实线表示，顶点写上规定的字母）．
（1）在图甲中画一个矩形EFGH．
（2）在图乙中画一个菱形MNPQ．
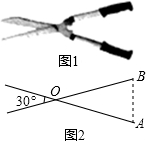17．如图1是一把园林剪刀，把它抽象为图2，其中OA=OB．若剪刀张开的角为30°，则∠A=75度．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网