题目内容
18.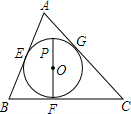 如图所示,⊙O是等边△ABC的内切圆,切点分别为E、F、G,P是$\widehat{EG}$上任意一点,则∠EPF的度数等于( )
如图所示,⊙O是等边△ABC的内切圆,切点分别为E、F、G,P是$\widehat{EG}$上任意一点,则∠EPF的度数等于( )| A. | 120° | B. | 90° | C. | 60° | D. | 30° |
分析 连接PE,OE,由等边三角形的性质得到∠B=60°,根据切线的性质得到∠BFO=∠BEO=90°,根据四边形的内角和得到∠EOF=120°,根据圆周角定理即可得到结论.
解答  解:连接PE,OE,
解:连接PE,OE,
∵△ABC是等边三角形,
∴∠B=60°,
∵⊙O是等边△ABC的内切圆,
∴∠BFO=90°,
∴∠EOF=120°,
∴∠EPF=$\frac{1}{2}∠$EOF=60°,
故选C.
点评 本题考查了三角形的内切圆与内心,切线的性质,圆周角定理,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
9.下列计算正确的是( )
| A. | a2•a3=a6 | B. | (a2)3÷(a3)3=1 | C. | (a2b)3÷(-ab)2=-a4b | D. | (a3)2•a5=a11 |
 作图题:
作图题: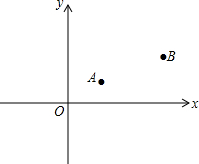 如图,已知A、B两村庄的坐标分别为A(2,2),B(7,4),一辆汽车在x轴上行驶,从原点O出发.
如图,已知A、B两村庄的坐标分别为A(2,2),B(7,4),一辆汽车在x轴上行驶,从原点O出发.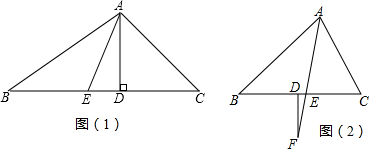
 用直尺和圆规作一个角等于已知角的示意图如图所示,则说明∠A′O′B′=∠AOB的依据是SSS(填SSS,SAS,AAS,ASA中的一种).
用直尺和圆规作一个角等于已知角的示意图如图所示,则说明∠A′O′B′=∠AOB的依据是SSS(填SSS,SAS,AAS,ASA中的一种).