题目内容
18. 如图,正方形ABCD的边长为12,AE=ED,2CP=PE,求阴影部分的面积.
如图,正方形ABCD的边长为12,AE=ED,2CP=PE,求阴影部分的面积.
分析 根据△DEF∽△BCF,得到$\frac{EF}{CF}=\frac{DE}{BC}$=$\frac{DB}{BF}$=$\frac{1}{2}$,得到EF=$\frac{1}{2}$CF,由于2CP=PE,证得EF=PF=PC,然后根据三角形的面积公式即可得到结果.
解答 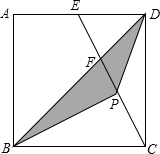 解:设BD,CE相交于F,
解:设BD,CE相交于F,
∵四边形ABCD是正方形,
∴BC=AD,AD∥BC,
∴△DEF∽△BCF,
∴$\frac{EF}{CF}=\frac{DE}{BC}$,
∵AE=ED,
∴DE=$\frac{1}{2}$BC,
∴$\frac{EF}{CF}$=$\frac{1}{2}$,
∴EF=$\frac{1}{2}$CF,
∵2CP=PE,
∴EF=PF=PC,
∵S△CDE=$\frac{1}{2}$DE•CD,
∴S△CDE=$\frac{1}{4}$S正方形ABCD=$\frac{1}{4}×12×12$=36,
∴S△DFP=$\frac{1}{3}$S△CDE=12,
∵△DEF∽△BCF,
∴$\frac{DF}{BF}=\frac{DE}{BC}=\frac{1}{2}$,
∴S△BPF=2S△PFD=24,
∴S△PBD=S△PBF+S△PDF=36.
∴阴影部分的面积=36.
点评 本题考查了相似三角形的判定和性质,三角形的面积,熟练掌握相似三角形的判定和性质定理是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
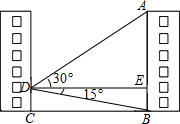 如图,小明站在家中窗口选一个观测点D,测得正对面AB楼顶端A的仰角为30°,楼底B的俯角为15°,观测点D到楼AB的距离为27米.(结果用根号表示)
如图,小明站在家中窗口选一个观测点D,测得正对面AB楼顶端A的仰角为30°,楼底B的俯角为15°,观测点D到楼AB的距离为27米.(结果用根号表示) 如图,?ABCD中,∠ABC=3∠A,F是CB的延长线上一点,EF⊥DC于E,CF=CD.若EF=3cm,求DE的长.
如图,?ABCD中,∠ABC=3∠A,F是CB的延长线上一点,EF⊥DC于E,CF=CD.若EF=3cm,求DE的长.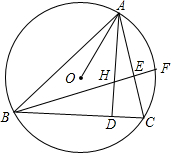 如图,△ABC的三个顶点都在⊙O上,AD、BE是△ABC的高,交于点H,BE的延长线交⊙O于F,下列结论:
如图,△ABC的三个顶点都在⊙O上,AD、BE是△ABC的高,交于点H,BE的延长线交⊙O于F,下列结论: