��Ŀ����
��ͼ����ƽ��ֱ������ϵ�У���֪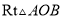 ������ֱ�DZ�
������ֱ�DZ�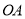 ��
��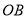 �ֱ���
�ֱ���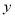 ���
���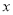 ���ϣ�
���ϣ� 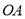 ��
��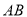 �ij��ֱ��Ƿ���
�ij��ֱ��Ƿ���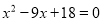 ������������
������������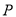 �ӵ�
�ӵ�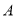 ��ʼ���߶�
��ʼ���߶�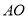 ����ÿ��
����ÿ��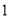 ����λ���ȵ��ٶ����
����λ���ȵ��ٶ����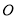 �˶���ͬʱ������
�˶���ͬʱ������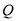 �ӵ�
�ӵ�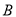 ��ʼ���߶�
��ʼ���߶�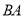 ����ÿ��
����ÿ��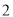 ����λ���ȵ��ٶ����
����λ���ȵ��ٶ����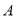 �˶������
�˶������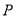 ��
��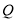 �˶���ʱ��Ϊ
�˶���ʱ��Ϊ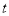 �룮
�룮
��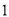 ����
����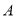 ��
��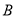 ��������꣮
��������꣮
��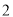 ����
����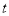 Ϊ��ֵʱ
Ϊ��ֵʱ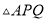 Ϊֱ�������Σ���ʱ��
Ϊֱ�������Σ���ʱ��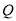 ������Ϊ��
��������
��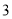 ����
����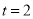 ʱ��������ƽ���ڣ��Ƿ���ڵ�
ʱ��������ƽ���ڣ��Ƿ���ڵ�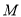 ��ʹ��
��ʹ��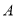 ��
��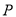 ��
��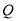 ��
��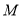 Ϊ������ı�����ƽ���ı��Σ������ڣ����
Ϊ������ı�����ƽ���ı��Σ������ڣ����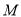 ������ꣻ�������ڣ���˵�����ɣ�
������ꣻ�������ڣ���˵�����ɣ�
��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ


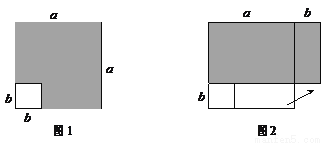
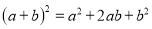
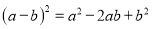
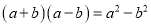

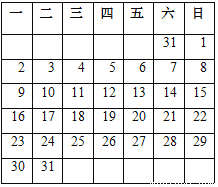

 �������⼯�������ϱ�ʾ������
�������⼯�������ϱ�ʾ������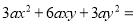 __________��
__________��