题目内容
16.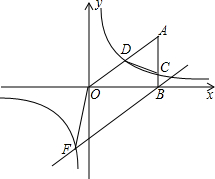 如图,AB⊥x轴于点B(8,0),$sin∠AOB=\frac{3}{5}$,反比例函数$y=\frac{m}{x}$与OA、AB分别相交于点D、C,且点D为OA的中点,
如图,AB⊥x轴于点B(8,0),$sin∠AOB=\frac{3}{5}$,反比例函数$y=\frac{m}{x}$与OA、AB分别相交于点D、C,且点D为OA的中点,(1)求反比例函数的解析式
(2)过点B的直线$y=\frac{3}{5}x+n$与反比例函数$y=\frac{m}{x}$图象交于第三象限内一点F,求四边形OABF的面积.
分析 (1)过点D作DM⊥x轴,通过正弦函数得出AB的长,即可得出A的坐标,进而得出D的坐标,代入$y=\frac{m}{x}$根据待定系数法即可求得;
(2)易求得直线BF的解析式,然后联立方程求得F的坐标,过点F作FN⊥x轴,根据S四边形OFBA=S△AOB+S△BOF求得即可.
解答 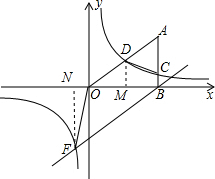 解:(1)过点D作DM⊥x轴,
解:(1)过点D作DM⊥x轴,
∵B(8,0),$sin∠AOB=\frac{3}{5}$,
∴AB=6,A(8,6),
又点D为OA的中点,
∴D(4,3),
∴反比例函数的解析式为$y=\frac{12}{x}$;
(2)∵直线$y=\frac{3}{5}x+n$过B点,
∴0=$\frac{3}{5}$×8+n,解得n=-$\frac{24}{5}$,
∴BF的解析式为$y=\frac{3}{5}x-\frac{24}{5}$,
解$\left\{\begin{array}{l}{y=\frac{3}{5}x-\frac{24}{5}}\\{y=\frac{12}{x}}\end{array}\right.$得$\left\{\begin{array}{l}{x=-2}\\{y=-6}\end{array}\right.$或$\left\{\begin{array}{l}{x=4}\\{y=3}\end{array}\right.$,
∴F(-2,-6),
过点F作FN⊥x轴,则S四边形OFBA=S△AOB+S△BOF=48.
点评 此题考查了反比例函数与一次函数的交点问题,锐角三角函数定义,以及坐标与图形性质,利用了待定系数法,待定系数法是常用的一种解题方法.同学们要熟练掌握这种方法.

练习册系列答案
相关题目
6.已知三角形的三边长为a、b、c,由下列条件能构成直角三角形的是( )
| A. | a2=(m-1)2,b2=4m2,c2=(m+1)2 | B. | a2=(m-1)2,b2=4m,c2=(m+1)2 | ||
| C. | a2=(m-1)2,b2=2m,c2=(m+1)2 | D. | a2=(m-1)2,b2=2m2,c2=(m+1)2 |
11.下列的计算正确的是( )
| A. | a(a-1)=a2-1 | B. | (x-2)(x+4)=x2-8 | C. | (x+2)2=x2+4 | D. | (x-2)(x+2)=x2-4 |
5.在-2,0,-0.5,3,$\frac{2}{3}$中,负数的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
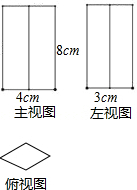 一个直四棱柱的三视图如图所示,俯视图是一个菱形,求这个直四棱柱的表面积.
一个直四棱柱的三视图如图所示,俯视图是一个菱形,求这个直四棱柱的表面积.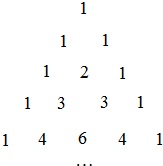 如图为杨辉三角表,它可以帮助我们按某种规律写出(a+b)n(n为自然数)展开式的系数,如:
如图为杨辉三角表,它可以帮助我们按某种规律写出(a+b)n(n为自然数)展开式的系数,如: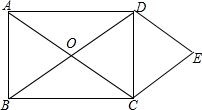 已知矩形ABCD中,对角线AC与BD相交于点O.分别过点D、C作AC、BD的平行线交于点E.
已知矩形ABCD中,对角线AC与BD相交于点O.分别过点D、C作AC、BD的平行线交于点E.