题目内容
14.已知抛物线y=x2-3x+m与x轴只有一个公共点,则m=$\frac{9}{4}$.分析 令y=0,则关于x的一元二次方程x2-x+m=0的根的判别式△=0,据此列出关于m的新方程,通过解新方程即可求得m的值.
解答 解:令y=0,则当抛物线y=x2-3x+m与x轴只有一个公共点时,关于x的一元二次方程x2-3x+m=0的根的判别式△=0,即(-3)2-4m=0,
解得:m=$\frac{9}{4}$.
故答案是:$\frac{9}{4}$.
点评 本题考查了抛物线与x轴的交点.解题时,运用“二次函数y=ax2+bx+c与x轴的交点个数与系数的关系:当b2-4ac=0时,只有一个交点”求解即可.

练习册系列答案
相关题目
20.下列命题是假命题的是( )
| A. | 平行四边形的对边相等 | |
| B. | 对角线互相平分的四边形是平行四边形 | |
| C. | 四条边都相等的四边形是菱形 | |
| D. | 矩形的对角线互相垂直 |
9.关于x的一元二次方程ax2-x+1=0有实数根,则a的取值范围是( )
| A. | a≤$\frac{1}{4}$且a≠0 | B. | a≤$\frac{1}{4}$ | C. | a≥$\frac{1}{4}$且a≠0 | D. | a≥$\frac{1}{4}$ |
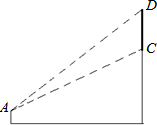 合肥新桥国际机场出港大厅有一幅“黄山胜景”的壁画.聪聪站在距壁画水平距离15米的地面,自A点看壁画上部D的仰角为45°,看壁画下部C的仰角为30°,求壁画CD的高度.(参考数据:$\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4,精确到十分位)
合肥新桥国际机场出港大厅有一幅“黄山胜景”的壁画.聪聪站在距壁画水平距离15米的地面,自A点看壁画上部D的仰角为45°,看壁画下部C的仰角为30°,求壁画CD的高度.(参考数据:$\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4,精确到十分位)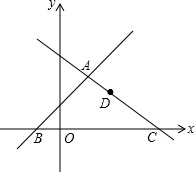 如图,在平面直角坐标系xOy中,直线l1:y=x+1与直线l2:y=kx+3交于点A,分别交x轴于点B和点C(4,0),点D是直线l2上的一个动点,
如图,在平面直角坐标系xOy中,直线l1:y=x+1与直线l2:y=kx+3交于点A,分别交x轴于点B和点C(4,0),点D是直线l2上的一个动点,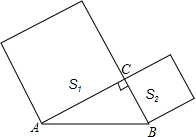 如图,已知在Rt△ABC中,∠ACB=90°,AB=4,分别以AC,BC为边向外作正方形,面积分别记为S1,S2,则S1+S2的值等于16.
如图,已知在Rt△ABC中,∠ACB=90°,AB=4,分别以AC,BC为边向外作正方形,面积分别记为S1,S2,则S1+S2的值等于16.