题目内容
18．已知a，b，c均为实数且$\sqrt{a^{2}-2a+1}$+|b+1|+（c+2）2=0，求方程ax2+bx+c=0的根．分析 根据非负数的性质得出a、b、c的性质，代入方程，利用因式分解法求解可得．
解答 解：∵$\sqrt{a^{2}-2a+1}$+|b+1|+（c+2）2=0，
∴a=1，b=-1，c=-2，
则方程为：x2-x-2=0，
即（x+1）（x-2）=0，
∴x+1=0或x-2=0，
解得：x=-1或x=2．
点评 本题主要考查解方程的能力和非负数的性质，根据非负数的性质得出a、b、c的值还原方程是解题的关键．
练习册系列答案
相关题目
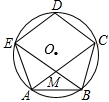如图，正五边形ABCDE的对角线AC，BE相交于M，求证：四边形CDEM是菱形．
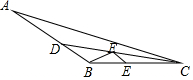如图，△ABC中，∠ACB=150°，CD是角平分线，BC=a，AC=b，AB=c，点E、F分别是BC、CD上两点，则BF+EF的最小值是$\frac{ac}{2b}$（用含a、b、c的代数式表示）
如图，∠ADC=90°，E是AC的中点，BE=DE．求证：AB⊥BC．