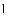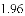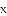��Ŀ����
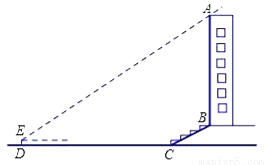
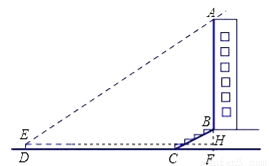
ijУ��ȤС�������һ����¥AB�ĸ߶ȣ���ͼ6����¥ǰ��һ��б��BC����֪BC�ij�Ϊ12�ף������¶�i=1��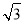 ������C��40��D�����ò���Dz�ô�¥����A������Ϊ37�㣬�����DE�ĸ�Ϊ1.5�ף����¥AB�ĸ߶�ԼΪ�����ף��������ȷ��0.1�ף�
������C��40��D�����ò���Dz�ô�¥����A������Ϊ37�㣬�����DE�ĸ�Ϊ1.5�ף����¥AB�ĸ߶�ԼΪ�����ף��������ȷ��0.1�ף�
���ο����ݣ�sin37���0.60��cos37���0.80��tan37���0.75��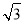 ��1.73����
��1.73����
���𰸡�33.3��
��������
����������ӳ�AB��ֱ��DC�ڵ�F������E��EH��AF������Ϊ��H����Rt��BCF�������¶ȵĶ������CF�ij�����DF������ã�Ȼ����ֱ�ǡ�AEH���������Ǻ������AF�ij����������AB�ij���
����������ӳ�AB��ֱ��DC�ڵ�F������E��EH��AF������Ϊ��H��
����Rt��BCF��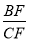 =i=1��
=i=1��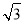 ������BF=k����CF=
������BF=k����CF=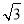 k��BC=2k��
k��BC=2k��
�֡�BC=12����k=6����BF=6��CF=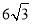 ����DF=DC+CF����DF=40+
����DF=DC+CF����DF=40+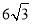 ������Rt��AEH��tan��AEH=
������Rt��AEH��tan��AEH=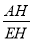 ����AH=tan37�����40+
����AH=tan37�����40+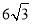 ����37.8���ף�����BH=BF��FH����BH=6��1.5=4.5����AB=AH��HB����AB=37.8��4.5=33.3��
����37.8���ף�����BH=BF��FH����BH=6��1.5=4.5����AB=AH��HB����AB=37.8��4.5=33.3��
�𣺴�¥AB�ĸ߶�ԼΪ33.3�ף�
���㣺1����ֱ�������ε�Ӧ��-���Ǹ������⣻2����ֱ�������ε�Ӧ��-�¶��½����⣮
�����͡������
��������
24
Ϊӭ�Ӱ�˳���������д���������ijУ����һ�չ�ˡ����������ļ�ֵ�ۡ�δ�����˻����������ǹ淶����֪ʶ��������ɼ���ΪA��B��C��D�ĸ��ȼ��������ռ������ݻ�����������������ͳ��ͼ.�������ͼ������������Ϣ��������и���:
(1)�����һ��ж����ˣ�
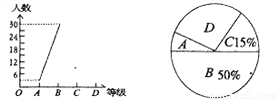
(2)��ȫ����ͳ��ͼ��
(3)������ͳ��ͼ�еȼ�Ϊ��D���IJ�����ռԲ�ĽǵĶ���Ϊ________��
(4)���ȼ�AΪ���㣬��ð��������.


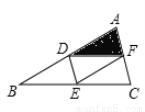
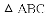
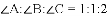
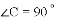 B.
B. 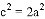 C.
C. 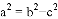 D.
D. 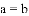
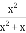 ��1����
��1����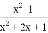 ������x��ֵ�Ӳ���ʽ��
������x��ֵ�Ӳ���ʽ��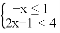 ����������ѡȡ��
����������ѡȡ��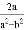 -
-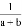 .
.