题目内容
如图，△ABC中，∠A=60°，则∠1+∠2的度数为（ ）| A、120° | B、180° |
| C、240° | D、300° |
考点：多边形内角与外角,三角形内角和定理
专题：计算题
分析：先由三角形内角和定理求出∠B+∠C的度数，再根据四边形内角和定理即可得出∠1+∠2的度数．
解答：解：根据三角形的内角和定理得：
四边形除去∠1，∠2后的两角的度数为180°-60°=120°，
则根据四边形的内角和定理得：
∠1+∠2=360°-120°=240°．
故选：C．
四边形除去∠1，∠2后的两角的度数为180°-60°=120°，
则根据四边形的内角和定理得：
∠1+∠2=360°-120°=240°．
故选：C．
点评：主要考查了三角形及四边形的内角和是360度的实际运用与三角形内角和180度之间的关系．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
已知点P1（x1，y1），P2（x2，y2），P3（x3，y3）在双曲线y=-
上，且x1＜x2＜0＜x3，则y1，y2，y3的大小关系为（ ）
| 2 |
| x |
| A、y1＜y2＜y3 |
| B、y3＜y1＜y2 |
| C、y2＜y3＜y1 |
| D、y3＞y2＞y1 |
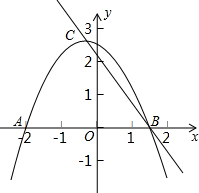已知二次函数y=ax2+bx+c（a≠0）的图象与x轴交于点A（-2，0）、B（x1，0），1＜x1＜2，与y轴正半轴的交点在（0，2）的上方，顶点为C，直线y=kx+m（k≠0）经过点C、B，下列结论：
如图所示，在菱形ABCD中，E、F分别是BC、CD上的点，且CE=CF