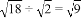题目内容
7.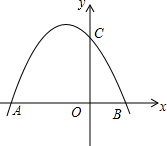 如图,已知抛物线y=ax2+bx+c与x轴交于点A(-6,0),B(2,0).
如图,已知抛物线y=ax2+bx+c与x轴交于点A(-6,0),B(2,0).(1)请用含a的式子表示c;
(2)若抛物线与y轴交于点C(0,4),求该抛物线的解析式;
(3)连接BC,在(2)的基础上,D为抛物线上的一点,连接OD,若∠DOC=∠ABC,求点D的横坐标.
分析 (1)把A和B的坐标代入抛物线的解析式,消去b即可求得a和c的关系;
(2)利用待定系数法即可求得函数的解析式;
(3)设D的横坐标是m,则纵坐标是-$\frac{1}{3}$m2-$\frac{4}{3}$m+4.过D作DE⊥y轴于点E.则△DOE∽△CBO,利用相似三角形的对应边的比相等即可列方程求解.
解答 解:(1)根据题意得:$\left\{\begin{array}{l}{36a-6b+c=0…①}\\{4a+2b+c=0…②}\end{array}\right.$,
①+②×3得:48a+4c=0,
即c=-12a;
(2)根据题意得:$\left\{\begin{array}{l}{36a-6b+c=0}\\{4a+2b+c=0}\\{c=4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{1}{3}}\\{b=-\frac{4}{3}}\\{c=4}\end{array}\right.$,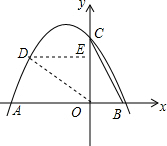
则抛物线的解析式是y=-$\frac{1}{3}$x2-$\frac{4}{3}$x+4;
(3)设D的横坐标是m,则纵坐标是-$\frac{1}{3}$m2-$\frac{4}{3}$m+4.
过D作DE⊥y轴于点E.
当m<0时,DE=-m,OE=-$\frac{1}{3}$m2-$\frac{4}{3}$m+4.
∵∠DEO=∠COB=90°,∠DOC=∠OBC,
∴△DOE∽△CBO,
∴$\frac{DE}{OC}$=$\frac{OE}{OB}$,即$\frac{-m}{4}$=$\frac{-\frac{1}{3}{m}^{2}-\frac{4}{3}m+4}{2}$,
解得:m=$\frac{-5-\sqrt{217}}{4}$或$\frac{-5+\sqrt{217}}{4}$(舍去).
当m>0时,DE=m,OE=-$\frac{1}{3}$m2-$\frac{4}{3}$m+4.
则$\frac{m}{4}$=$\frac{-\frac{1}{3}{m}^{2}-\frac{4}{3}m+4}{2}$,
解得:m=$\frac{-11+\sqrt{313}}{4}$或$\frac{-11-\sqrt{313}}{4}$(舍去).
总之,m的值是$\frac{-5-\sqrt{217}}{4}$或$\frac{-11+\sqrt{313}}{4}$.
点评 本题考查了待定系数法求函数的解析式以及相似三角形的判定与性质,正确作出辅助线构造相似三角形是关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图所示,已知CD∥AB,OE平分∠DOB,OE⊥OF,∠CDO=60°,求∠DOF的度数.
如图所示,已知CD∥AB,OE平分∠DOB,OE⊥OF,∠CDO=60°,求∠DOF的度数.
 的倒数是( )
的倒数是( ) B.
B.  C.
C. 
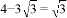 B.
B. 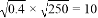 C.
C. 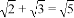 D.
D.