题目内容
18.春季流感爆发,某校为了解全体学生患流感情况,随机抽取部分班级对患流感人数的进行调查,发现被抽查各班级患流感人数只有1名、2名、3名、4名、5名、6名这六种情况,并制成如下两幅不完整的统计图:(1)抽查了20个班级,并将该条形统计图补充完整;
(2)如图1中患流感人数为4名所在扇形的圆心角的度数为72°;
(3)若该校有90个班级,请估计该校此次患流感的人数.
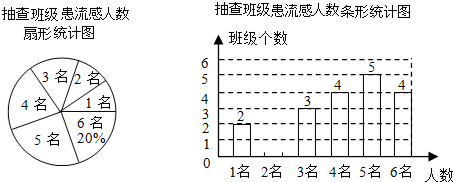
分析 (1)根据患流感人数有6名的班级有4个,占20%,可求得抽查的班级数,再减去其它班级数,即可补全统计图;
(2)用患流感人数为4名的班级4个除以抽查的班级数,再乘以360°即可;
(3)先求出该校平均每班患流感的人数,再利用样本估计总体的思想,用这个平均数乘以90即可.
解答 解:(1)抽查的班级个数为4÷20%=20(个),
患流感人数只有2名的班级个数为:20-(2+3+4+5+4)=2(个),
补图如下:
(2)根据题意得:$\frac{4}{20}$×360°=72°;
(3))∵该校平均每班患流感的人数为:(1×2+2×2+3×3+4×4+5×5+6×4)÷20=4,
∴若该校有90个班级,则此次患流感的人数为:4×90=360(人).
故答案为:(1)20;(2)72°.
点评 本题考查了条形统计图和扇形统计图以及利用样本估计总体的思想,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
相关题目
6.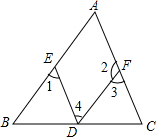 如图,在下列给出的条件中,不能判定AB∥DF的是( )
如图,在下列给出的条件中,不能判定AB∥DF的是( )
 如图,在下列给出的条件中,不能判定AB∥DF的是( )
如图,在下列给出的条件中,不能判定AB∥DF的是( )| A. | ∠A+∠2=180° | B. | ∠1=∠A | C. | ∠1=∠4 | D. | ∠A=∠3 |
9.观察下表:
(1)结合该表格及相关知识,求x,y;
(2)猜想第n行的三个数(用含n的式子表示),并证明它们是一组勾股数.
| 4 | 3 | 5 | 32+42=52 |
| 6 | 8 | 10 | 62+82=102 |
| 8 | 15 | 17 | 82+152=172 |
| 10 | 24 | 26 | 102+242=262 |
| … | … | … | … |
| 60 | x | y | 602+x2=y2 |
| … | … | … | … |
(2)猜想第n行的三个数(用含n的式子表示),并证明它们是一组勾股数.
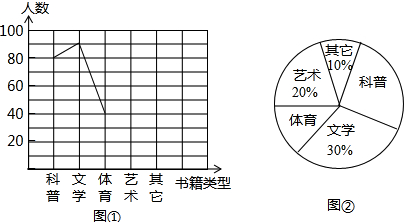
 如图所示,已知CD∥AB,OE平分∠DOB,OE⊥OF,∠CDO=60°,求∠DOF的度数.
如图所示,已知CD∥AB,OE平分∠DOB,OE⊥OF,∠CDO=60°,求∠DOF的度数.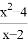 的值为零,那么x=__________.
的值为零,那么x=__________.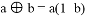 ,若a、b是方程
,若a、b是方程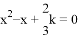 (k<0)的两根,则
(k<0)的两根,则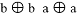 的值为______.
的值为______.