题目内容
6.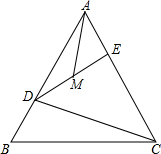 △ABC是等边三角形,D、E分别在AB、AC上,BD=AE,M是DE的中点,连结AM,CD.求证:CD=2AM.
△ABC是等边三角形,D、E分别在AB、AC上,BD=AE,M是DE的中点,连结AM,CD.求证:CD=2AM.
分析 作DF∥AC交BC于F,DG∥BC交AC于G,利用等边三角形的性质和全等三角形的判定证明即可.
解答 证明:作DF∥AC交BC于F,DG∥BC交AC于G,连接FG交CD于N,则四边形CFDG是平行四边形,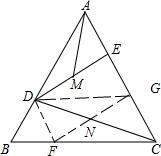
∴CN=CN=$\frac{1}{2}$CD,NF=NG,CG=DF,
∵△ABC是等边三角形,
∴AB=BC,∠B=∠BAC=∠BCA=60°,
∴∠B=∠BDF=∠BFD=60°,
∴BD=BF=DF=AE=CG,
∴AD=CF,
在△ADE与△CFG中,
$\left\{\begin{array}{l}{AD=CF}\\{∠DAE=∠FCG=60°}\\{AE=CG}\end{array}\right.$,
∴△ADE≌△CFG(SAS),
∵AM、CN分别是△ADE与△CFG的对应中线,
∴AM=CN,
∴CD=CN=2AM.
点评 此题考查全等三角形的判定和性质,关键是利用等边三角形的性质和全等三角形的判定证明.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
14. 如图,直线a∥b∥c,∠1=100°,∠2=135°,那么∠α等于( )
如图,直线a∥b∥c,∠1=100°,∠2=135°,那么∠α等于( )
 如图,直线a∥b∥c,∠1=100°,∠2=135°,那么∠α等于( )
如图,直线a∥b∥c,∠1=100°,∠2=135°,那么∠α等于( )| A. | 45° | B. | 55° | C. | 60° | D. | 70° |
11.下列四个命题中是真命题的是( )
| A. | 相等的角是对顶角 | |
| B. | 两条直线被第三条直线所截,同位角相等 | |
| C. | 实数与数轴上的点是一一对应的 | |
| D. | 垂直于同一条直线的两条直线互相平行 |
18.长方体的顶点数、棱数、面数分别是( )
| A. | 8 10 6 | B. | 6 12 8 | C. | 6 8 10 | D. | 8 12 6 |
 是由五个大小相同的小方块拼凑而成的,问:
是由五个大小相同的小方块拼凑而成的,问: