题目内容

8．已知一直线过点（3，2）和（-1，-2），求该直线的解析式．

分析 设直线解析式为y=kx+b，然后把两个点的坐标代入得到关于k、b的方程组，然后解方程组即可．

解答 解：设直线解析式为y=kx+b，
把（3，2）、（-1，-2）分别代入得$\left\{\begin{array}{l}{3k+b=2}\\{-k+b=-2}\end{array}\right.$，解得$\left\{\begin{array}{l}{k=1}\\{b=-1}\end{array}\right.$，
所以直线解析式为y=x-1．

点评 本题考查了待定系数法求一次函数解析式：先设出函数的一般形式，如求一次函数的解析式时，先设y=kx+b；将自变量x的值及与它对应的函数值y的值代入所设的解析式，得到关于待定系数的方程或方程组；解方程或方程组，求出待定系数的值，进而写出函数解析式．

练习册系列答案
相关题目
18．已知一元二次方程x2-4=0，则该方程的解为（　　）
A．x1=x2=2B．x1=x2=-2C．x1=-4，x2=4D．x1=-2，x2=2
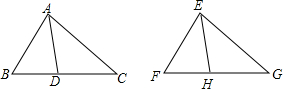19．如图，已知△ABC和△EFG中，∠BAC=∠FEC，∠B=∠F，AD、EH分别是∠BAC、∠FEC的平分线，且AD=EH．求证：△ABC≌△EFG．
16．一辆客车从甲地行驶到乙地，同时一辆货车沿同一线路从乙地行驶到甲地，两车出发1h时相距510km，出发3h时相距170km（均指相遇以前的距离），假设两车均为匀速行驶．
（1）求甲、乙两地之间的距离；
（2）若客车将速度提高6km/h，则从甲地到乙地可节省3h，求客车原来的速度．
3．已知：如图AE=AD，∠B=∠C，△ABD与△ACE全等吗？为什么？
13．已知两个样本数据如下：
甲：9.8、9.9、10.3、10.1、10.4、9.7、9.8
乙：10.5、9.6、10.1、9.8、9.5、10.2、10、10.3
分别计算两个样本的方差，并比较哪一个样本数据较稳定？
20．计算：
（1）（xy-x2）÷$\frac{x-y}{xy}$；
（2）$\frac{x}{{x}^{2}-3x}$•（x2-9）
17．先阅读下列材料，然后再解答问题：
解不等式：|x|＜3
通过对x的符号讨论，可将原不等式中的绝对值符号去掉，当x≥0时，|x|=x，|x|＜3即为x＜3．此时原不等式满足两个条件x≥0和x＜3，即$\left\{\begin{array}{l}{x≥0}\\{x＜3}\end{array}\right.$，当x＜0时，|x|=-x，|x|＜3即为-x＜3．此时原不等式满足两个条件x＜0和-x＜3，即$\left\{\begin{array}{l}{x＜0}\\{-x＜3}\end{array}\right.$．∴原不等式|x|＜3可化为两个不等式组：$\left\{\begin{array}{l}{x≥0}\\{x＜3}\end{array}\right.$或$\left\{\begin{array}{l}{x＜0}\\{-x＜3}\end{array}\right.$，解这两个不等式组得：0≤x＜3或-3＜x＜0．在数轴上表示出来为：
两部分解集合起来即为|x|＜3的解集．即|x|＜3的解集为-3＜x＜3．
（1）直接写出不等式：|2x-1|＜3的解集；
（2）解不等式：x+|2x-1|＞3．
（3）解不等式：|x|+|2x-1|＜3需化成几个不等式组？解出该不等式．
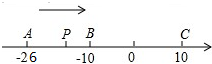2．已知数轴上有A、B、C三点，分别表示有理数-26，-10，10，动点P从
A出发，以每秒1个单位的速度向终点C移动，设点P移动时间为t秒．
（1）用含t的代数式表示P到点A和点C的距离：PA=t，PC=36-t
（2）当点P运动到B点时，点Q从A点出发，以每秒3个单位的速度向C点运动，Q点到达C点后，再立即以同样的速度返回，当点P运动到点C时，P、Q两点运动停止，
①当P、Q两点运动停止时，求点P和点Q的距离；
②求当t为何值时P、Q两点恰好在途中相遇．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网