题目内容
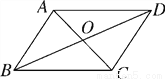
如图，?ABCD的对角线AC，BD相交于点O，且AC＋BD＝16，CD＝6，则△ABO的周长是( )
A. 10 B. 14 C. 20 D. 22
B
【解析】试题分析：∵四边形ABCD是平行四边形，∴AO=CO，BO=DO，DC=AB=6，∵AC+BD=16，∴AO+BO=8，∴△ABO的周长是：14．故选B．
学练快车道快乐假期暑假作业新疆人民出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案甲、乙原有存款800元和1800元，从本月开始，甲每月存400元，乙每月存200元．如果设两人存款时间为x月．甲存款额是y1元，乙存款额是y2元．
（1）试写出y1与x及y2与x之间的函数关系式；
（2）到第几个月时，甲存款额能超过乙存款额？
详见解析
【解析】
试题分析：（1）根据存款数=原有存款+又存入的钱数，列式即可；
（2）列出一元一次不等式，然后求解即可．
【解析】
（1）根据题意，甲：y1=400x+800，
乙：y2=200x+1800；
（2）根据题意，400x+800＞200x+1800，
解得x＞5，
所以，从第6个月开始，甲存款额能超过乙存款额． 一个多边形的内角和是外角和的2倍，则这个多边形的边数为______．
6
【解析】∵多边形的外角和是360度，多边形的内角和是外角和的2倍，
则内角和是720度，
720÷180+2=6，
∴这个多边形是六边形，
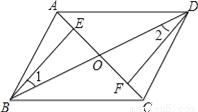
故答案为：6． 如图，四边形ABCD中，对角线AC，BD相交于点O，点E，F分别在OA，OC上
（1）给出以下条件；①OB=OD，②∠1=∠2，③OE=OF，请你从中选取两个条件证明△BEO≌△DFO；
（2）在（1）条件中你所选条件的前提下，添加AE=CF，求证：四边形ABCD是平行四边形．
（1）见解析；（2）见解析.
【解析】试题分析：（1）选取①②，利用ASA判定△BEO≌△DFO；也可选取②③，利用AAS判定△BEO≌△DFO；还可选取①③，利用SAS判定△BEO≌△DFO；
（2）根据△BEO≌△DFO可得EO＝FO，BO＝DO，再根据等式的性质可得AO＝CO，根据两条对角线互相平分的四边形是平行四边形可得结论．
试题解析：
证明：（1）选取①②，
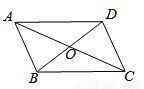
... 如图，四边形ABCD的对角线相交于点O，AO=CO，请添加一个条件_________
（只添一个即可），使四边形ABCD是平行四边形
BO=DO
【解析】【解析】
∵AO=CO，BO=DO，∴四边形ABCD是平行四边形．故答案为：BO=DO． 如图，在?ABCD中，AB＝6，BC＝8，∠BCD的平分线交AD于点E，交BA的延长线于点F，则AE＋AF的值等于( )
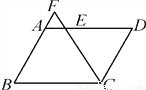
A. 2 B. 3 C. 4 D. 6
C
【解析】试题分析：由平行四边形的性质和角平分线得出∠F=∠FCB，证出BF=BC=8，同理：DE=CD=6，求出AF=BF﹣AB=2，AE=AD﹣DE=2，即可得出结果．∵四边形ABCD是平行四边形， ∴AB∥CD，AD=BC=8，CD=AB=6，
∴∠F=∠DCF，∵∠C平分线为CF，∴∠FCB=∠DCF，∴∠F=∠FCB， ∴BF=BC=8，
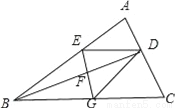
同理：DE=CD=6， ∴A... 如图，BD是△ABC的角平分线，它的垂直平分线分别交AB，BD，BC于点E，F，G，连接ED，DG．
（1）请判断四边形EBGD的形状，并说明理由；
（2）若∠ABC=30°，∠C=45°，ED=2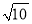
，点H是BD上的一个动点，求HG+HC的最小值．
（1）四边形EBGD是菱形，理由见解析；（2）.
【解析】试题分析：（1）四边形EBGD是菱形，根据已知条件易证△EFD≌△GFB，可得ED=BG，所以BE=ED=DG=GB，即可判定四边形EBGD是菱形．（2）作EM⊥BC于M，DN⊥BC于N，连接EC交BD于点H，此时HG+HC最小，在RT△EMC中，求出EM、MC即可解决问题．
试题解析：（1）四边形EBGD是菱形．
理由：... 如图，平行四边形ABCD的周长是26cm，对角线AC与BD交于点O，AC⊥AB，E是BC中点，△AOD的周长比△AOB的周长多3cm，则AE的长度为（ ）
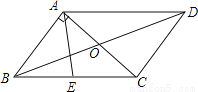
A. 3cm B. 4cm C. 5cm D. 8cm
B
【解析】试题解析：∵?ABCD的周长为26cm，
∴AB+AD=13cm，OB=OD，
∵△AOD的周长比△AOB的周长多3cm，
∴（OA+OD+AD）-（OA+OB+AB）=AD-AB=3cm，
∴AB=5cm，AD=8cm．
∴BC=AD=8cm．
∵AC⊥AB，E是BC中点，
∴AE=BC=4cm.
故选B． 已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列说法错误的是（ ）
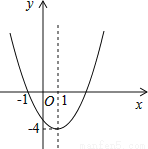
A．图象关于直线x=1对称
B．函数y=ax2+bx+c（a≠0）的最小值是﹣4
C．﹣1和3是方程ax2+bx+c=0（a≠0）的两个根
D．当x＜1时，y随x的增大而增大
D
【解析】
试题分析：根据对称轴及抛物线与x轴交点情况，结合二次函数的性质，即可对所得结论进行判断．
【解析】
A、观察图象，可知抛物线的对称轴为直线x=1，则图象关于直线x=1对称，正确，故本选项不符合题意；
B、观察图象，可知抛物线的顶点坐标为（1，﹣4），又抛物线开口向上，所以函数y=ax2+bx+c（a≠0）的最小值是﹣4，正确，故本选项不符合题意；
C、...