��Ŀ����
14����ͼ1�����ı���ABCD��AB������ȡһ��E����E�����A����B�غϣ��ֱ�����ED��EC�������ı���ABCD�ֳ�3�������Σ����������2�����������ƣ����ǾͰѵ�E�����ı���ABCD��AB���ϵ����Ƶ㣻�����3�������ζ����ƣ����ǾͰѵ�E�����ı���ABCD��AB���ϵ�ǿ���Ƶ㣮��1����ͼ1�У���A=��B=��DEC=50�㣬֤����E���ı���ABCD��AB���ϵ����Ƶ㣮
��2������ͼ2����������ABCD��AB���ϵ�һ��ǿ���Ƶ㣮��Ҫ��ͼ���߲��ޣ���д������������ͼ�ۼ����б�Ҫ��˵����
�ڶ��������һ�����Σ��Ƿ�һ������ǿ���Ƶ㣿���һ�����ڣ���˵�����ɣ������һ�����ڣ���ٳ�������
��3����ͼ3�����ı���ABCD�У�AD��BC��AD��BC����B=90�㣬��E���ı���ABCD��AB���ϵ�һ��ǿ���Ƶ㣬�ж�AE��BE��������ϵ��˵�����ɣ�
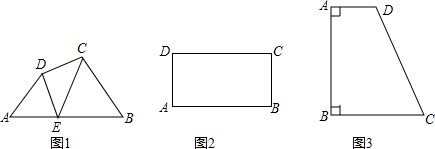
���� ��1��Ҫ֤����E���ı���ABCD��AB���ϵ����Ƶ㣬ֻҪ֤����һ�����������ƾ��У�������֤����ADE�ס�EBC����������ý⣻
��2������CDΪֱ��������ȡ�û���AB��һ�����㼴Ϊ���ڲ�һ������ǿ���Ƶ㣬�������Σ�
��3����Ϊ��E������ABCD��AB���ϵ�һ��ǿ���Ƶ㣬���Ծ������������γ��֣��������������εĶ�Ӧ�߶γɱ����������жϳ�AE��BE��������ϵ���Ӷ�������⣮
��� �⣺��1�����ɣ��ߡ�A=50�㣬
���ADE+��DEA=130�㣬
�ߡ�DEC=50�㣬
���BEC+��DEA=130�㣬
���ADE=��BEC��
�ߡ�A=��B��
���ADE�ס�BEC��
���E���ı���ABCD��AB���ϵ����Ƶ㣻
��2������CDΪֱ��������ȡ�û���AB��һ�����㼴Ϊ����
��ͼ2��ʾ������FC��DF��
��CDΪֱ�������DFC=90�㣬
��CD��AB��
���DCF=��CFB��
�ߡ�B=90�㣬
���DFC�ס�CBF��
ͬ���ɵó�����DFC�ס�FAD��
�ڶ��������һ�����Σ���һ������ǿ���Ƶ㣬�������Σ�
��3����һ���������A=��B=��DEC=90�㣬��ADE=��BEC=��EDC��
����ADE�ס�BEC�ס�EDC��
�ߵ�E������ABCD�ı�AB�ϵ�ǿ���Ƶ㣬
���ADE����BEC�Լ���CDE���������Ƶģ�
�ߡ�ADE��ֱ�������Σ�
���DECҲ��ֱ�������Σ�
����DEC=90��ʱ��
�١�CDE=��DEA��
��DC��AE��
�����ı���ABCD��������ì�ܣ���������
�ڡ�CDE=��EDA��
�ߡ�ECD+��EDC=90�㣬��ADE+��AED=90�㣬
���AED=��ECD��
�ߡ�AED+��BEC=90�㣬��BEC+��BCE=90�㣬
���AED=��BCE��
���AED=��BCE=��ECD��
��DEƽ�֡�ADC��ͬ���ɵã�CEƽ�֡�DCB��
��ͼ3����E��EF��DC��
��AE��AD��BE��BC��DEƽ�֡�ADC��CEƽ�֡�DCB��
��AE=FE��BE=FE��
��AE=BE��
�ڶ����������A=��B=��EDC=90�㣬��ADE=��BCE=��DCE��
����ADE�ס�BEC�ס�DCE��
���ԡ�AED=��BEC=��DEC=60�㣬
˵��AE=$\frac{1}{2}$DE��BE=$\frac{1}{2}$CE��DE=$\frac{1}{2}$CE��
����AE=$\frac{1}{2}$BE��
���ϣ�AE=BE��AE=$\frac{1}{2}$BE��
���� ���⿼�������������ε��ж������ʡ����ε����ʡ����ε������Լ��������Ƶ��ǿ���Ƶ�ĸ������ǿ���Ƶ�ĸ����ȷ������ص��ж����������ʶ����ǽ���Ĺؼ���ע����������˼�����ȷ���ã�

 ��У����ϵ�д�
��У����ϵ�д�| A�� | 4 | B�� | 5 | C�� | 6 | D�� | 8 |
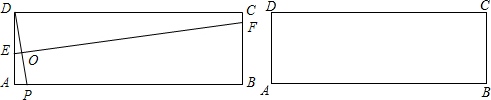
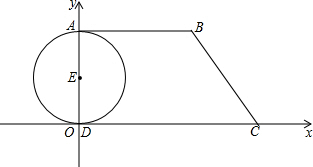 ��ͼ����ƽ��ֱ������ϵ�У�ֱ������ABCD��ֱ�Ƕ���D��ԭ���غϣ���һֱ�Ƕ���A��y����������ϣ���B��C������ֱ�ΪB��12��8����C��14��0����ADΪ��E��ֱ������M��N�ֱ��A��C����ͬʱ�����������˶������е�M��AB���յ�B�˶����ٶ�Ϊÿ��1����λ����N��CD���յ�D�˶����ٶ�Ϊÿ��3����λ��������������һ�㵽���Լ����յ�ʱ����һ��Ҳֹͣ�˶���
��ͼ����ƽ��ֱ������ϵ�У�ֱ������ABCD��ֱ�Ƕ���D��ԭ���غϣ���һֱ�Ƕ���A��y����������ϣ���B��C������ֱ�ΪB��12��8����C��14��0����ADΪ��E��ֱ������M��N�ֱ��A��C����ͬʱ�����������˶������е�M��AB���յ�B�˶����ٶ�Ϊÿ��1����λ����N��CD���յ�D�˶����ٶ�Ϊÿ��3����λ��������������һ�㵽���Լ����յ�ʱ����һ��Ҳֹͣ�˶���