题目内容
解下列方程组(不等式组):
(1)
;
(2)解不等式(组)
,并把解集在数轴上表示出来.
(1)
|
(2)解不等式(组)
|
考点:解三元一次方程组,在数轴上表示不等式的解集,解一元一次不等式组
专题:计算题
分析:(1)方程组利用加减消元法求出解即可;
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分即可.
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分即可.
解答:解:(1)
,
①+②得:5x+2y=16④;
②+③得:3x+4y=18⑤,
④×2-⑤得:7x=14,即x=2,
将x=2代入④得:y=3,
将x=2,y=3代入③得:z=1,
则方程组的解为
;
(2)
,
由①得:x>-1;
由②得:x≤2,
则方程组的解为-1<x≤2.
|
①+②得:5x+2y=16④;
②+③得:3x+4y=18⑤,
④×2-⑤得:7x=14,即x=2,
将x=2代入④得:y=3,
将x=2,y=3代入③得:z=1,
则方程组的解为
|
(2)
|
由①得:x>-1;
由②得:x≤2,
则方程组的解为-1<x≤2.
点评:此题考查了解三元一次方程组,以及解一元一次不等式组,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
 点A某地下车库出口处“两段式栏杆”转动的支点,点E栏杆两段的连接点.当车辆经过时,栏杆AEF的位置如图所示,其中AB⊥BC,EF∥BC,∠EAB=133°,AB=AE=1.2,栏杆EF段距离地面的高度(即直线EF上任意一点到直线BC的距离).
点A某地下车库出口处“两段式栏杆”转动的支点,点E栏杆两段的连接点.当车辆经过时,栏杆AEF的位置如图所示,其中AB⊥BC,EF∥BC,∠EAB=133°,AB=AE=1.2,栏杆EF段距离地面的高度(即直线EF上任意一点到直线BC的距离). 如图,已知点E是梯形ABCD下底BC的中点,点E到两腰的距离EM,EN相等.求证:AB=DC.
如图,已知点E是梯形ABCD下底BC的中点,点E到两腰的距离EM,EN相等.求证:AB=DC. 如图,点O是菱形ABCD对角线的交点,CE∥BD,EB∥AC,连接OE,交BC于F.
如图,点O是菱形ABCD对角线的交点,CE∥BD,EB∥AC,连接OE,交BC于F. 以直线C为对称轴,画出下图的另一半.
以直线C为对称轴,画出下图的另一半.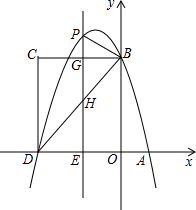 如图,在平面直角坐标系中,抛物线y=-
如图,在平面直角坐标系中,抛物线y=-