题目内容
6．先化简，再求值：a（a-2b）+2（a+b）（a-b）+（a+b）2，其中a，b满足|a+$\frac{1}{2}}$|+（b-1）2=0．分析 先算乘法，再合并同类项，求出a、b后代入求出即可．
解答 解：a（a-2b）+2（a+b）（a-b）+（a+b）2
=a2-2ab+2a2-2b2+a2+2ab+b2
=4a2-b2，
∵|a+$\frac{1}{2}}$|+（b-1）2=0，
∴a+$\frac{1}{2}$=0，b-1=0，
a=-$\frac{1}{2}$，b=1，
原式=4×（-$\frac{1}{2}$）2-12=0．
点评 本题考查了整式的混合运算和求值，绝对值和偶次方的非负性的应用，能正确根据整式的运算法则进行化简是解此题的关键．
练习册系列答案
相关题目
17．
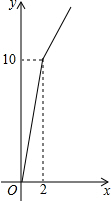某玉米种子的价格为a元/千克，如果一次购买2千克以上的种子，超过2千克部分的种子价格打8折．某科技人员对付款金额和购买量这两个变量的对应关系用列表法做了分析，并绘制出函数图象．如表是该科技人员绘制的图象和表格的不完整资料，已知点A的坐标为（2，10）．请你结合表格和图象：
（1）指出付款金额和购买量哪个变量是函数的自变量x，并直接写出表中a、b的值；
（2）求出当x＞2时，y关于x的函数解析式；
（3）甲农户将8.8元钱全部用于购买玉米种子，乙农户购买了4500克该玉米种子，分别计算他们的购买量和付款金额．
某玉米种子的价格为a元/千克，如果一次购买2千克以上的种子，超过2千克部分的种子价格打8折．某科技人员对付款金额和购买量这两个变量的对应关系用列表法做了分析，并绘制出函数图象．如表是该科技人员绘制的图象和表格的不完整资料，已知点A的坐标为（2，10）．请你结合表格和图象：| 付款金额（元） | a | 7.5 | 10 | 12 | b |
| 购买量（千克） | 1 | 1.5 | 2 | 2.5 | 3 |
（2）求出当x＞2时，y关于x的函数解析式；
（3）甲农户将8.8元钱全部用于购买玉米种子，乙农户购买了4500克该玉米种子，分别计算他们的购买量和付款金额．
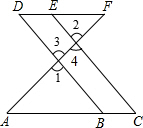填空：如图，E点为DF上的点，B为AC上的点，已知∠1=∠2，∠C=∠D，说明DF∥AC的理由．
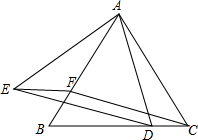如图，△ABC为等边三角形，D、F分别为BC、AB上的点，且CD=BF．
已知：如图，点E是线段AB的中点，∠A=∠B，∠AED=∠BEC．求证：CE=DE．