Question

12．在Rt△ABC中，∠BAC=90°，D是BC的中点，E是AD的中点，过点A作AF∥BC交BE的延长线于点F．
（1）证明四边形ADCF是菱形；
（2）若AC=4，AB=5，求菱形ADCF的面积．

Answer 1

分析 （1）首先根据题意画出图形，由E是AD的中点，AF∥BC，易证得△AFE≌△DBE，即可得AF=BD，又由在Rt△ABC中，∠BAC=90°，D是BC的中点，可得AD=BD=CD=AF，证得四边形ADCF是平行四边形，继而判定四边形ADCF是菱形；
（2）首先连接DF，易得四边形ABDF是平行四边形，即可求得DF的长，然后由菱形的面积等于其对角线积的一半，求得答案．

解答 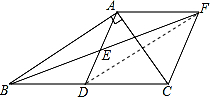（1）证明：如图，∵AF∥BC，
∴∠AFE=∠DBE，
∵E是AD的中点，AD是BC边上的中线，
∴AE=DE，BD=CD，
在△AFE和△DBE中，
$\left\{\begin{array}{l}{∠AFE=∠DBE}\\{∠FEA=∠BED}\\{AE=DE}\end{array}\right.$，
∴△AFE≌△DBE（AAS）；
∴AF=DB．
∵DB=DC，
∴AF=CD，
∴四边形ADCF是平行四边形，
∵∠BAC=90°，D是BC的中点，
∴AD=DC=$\frac{1}{2}$BC，
∴四边形ADCF是菱形；

（2）解：连接DF，
∵AF∥BC，AF=BD，
∴四边形ABDF是平行四边形，
∴DF=AB=5，
∵四边形ADCF是菱形，
∴S=$\frac{1}{2}$AC•DF=10．

点评 此题考查了菱形的判定与性质以及全等三角形的判定与性质．注意根据题意画出图形，结合图形求解是关键．