题目内容
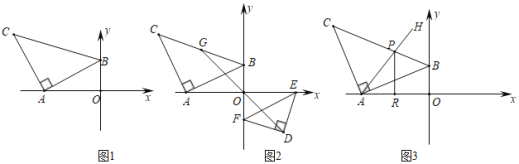
【题目】如图1，将任意一个等腰直角三角板△ABC放至平面直角坐标系xOy中，直角顶点A（a，0）在x轴的负半轴，点B（0，b）在y轴的正半轴，点C落在第二象限，
（1）若
＝﹣b2+4b﹣4，求C点坐标；
（2）如图2，再将任意的一个等腰直角三角板△DEF放至平面直角坐标系xOy中，点E在x轴的正半轴上，F在y轴的负半轴上，直角顶点D落在第四象限，设点G为BC的中点，证明：点D，O，G三点刚好在同一条直线上；
（3）已知a＝﹣4，b＜4.如图3，点O关于直线AB的对称点为点H，AH交线段BC于点P，PR⊥x轴于点R，求△APR的周长．
【答案】（1）C（﹣6，4）；（2）证明见解析；（3）△APR的周长＝8．
【解析】
（1）如图1中，作CH⊥OA于H.利用非负数的性质求出a，b，再利用全等三角形的性质解决问题即可．
（2）利用四点共圆证明∠AOG＝45°，∠DOE＝45°，推出∠AOG＝∠DOE即可．
（3）如图3中，连接BH，作BK⊥PR于K，在AO上截取AM，使得AM＝AP.利用全等三角形的性质证明PK＝PH，RK＝RO，可以推出△APR的周长＝AH+AO＝8．
解：（1）如图1中，作CH⊥OA于H．
∵
＝﹣b2+4b﹣4，
∴+（b﹣2）2＝0，
∵≥0，（b﹣2）2≥0，
∴2b+a＝0，b＝2，
∴a＝﹣4，
∴A（﹣4，0），B（0，2），
∴OA＝4，OB＝2，
∵∠CHA＝∠AOB＝∠CAB＝90°，
∴∠CAH+∠BAO＝90°，∠BAO+∠ABO＝90°，
∴∠CAH＝∠ABO，
∵AC＝AB，
∴△CHA≌△AOB（AAS），
∴CH＝OA＝4，AH＝OB＝2，
∴OH＝6，
∴C（﹣6，4）．
（2）如图2中，连接AG．
∵AC＝AB，CG＝GB，
∴AG⊥BC，∠ABC＝45°，
∴∠AGB＝∠AOB＝90°，
∴A，G，B，O四点共圆，
∴∠AOG＝∠ABC＝45°，
∵∠EOF＝∠EDF＝90°，
∴O，E，D，F四点共圆，
∴∠DOE＝∠DFE，
∵DE＝DF，∠EDF＝90°，
∴∠DFE＝45°，
∠DOF＝45°＝∠AOG，
∴D，O，G共线．
（3）如图3中，连接BH，作BK⊥PR于K，在AO上截取AM，使得AM＝AP．
∵AB＝AB，∠BAP＝∠BAM，AP＝AM，
∴△BAP≌△BAM（SAS），
∴BP＝BM，∠ABP＝∠ABM＝45°，
∴∠PBM＝90°，
∵∠H＝∠BOM＝90°，BP＝BM，BH＝BO，
∴Rt△BHP≌△BOM（HL），
∴∠BPH＝∠BMO，
∵∠PBM＝∠PRM＝90°，
∴∠BMO+∠AMB＝180°，∠AMB+∠RPB＝180°，
∴∠BPR＝∠BMO＝∠BPH，
∵BH⊥PH，BK⊥PR，
∴BH＝BK，∠H＝∠BKP＝90°，
∵PB＝PB，
∴Rt△BPH≌Rt△BPK（HL），
∴PK＝PH，
∵BO＝BH，
∴BK＝BO，
∵∠BKR＝∠KRO＝∠ROB＝90°，
∴四边形OBKR是矩形，
∵BO＝BK，
四边形BORK是正方形，
∴RK＝OR，
∴AO＝AH＝4，
∴△APR的周长＝AP+PK+KR+AR＝AH+AO＝8．
