Question

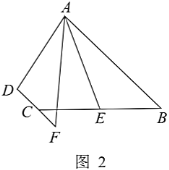
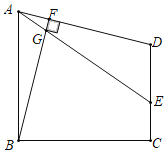
【题目】在四边形ABCD中，∠ABC＝∠DCB＝90°，AB＝BC.过点B作BF⊥AD，垂足为点F，

（1）求证：∠DAB＝∠FBC；

（2）点E为线段CD上的一点，连接AE交BF于G，若∠BAE+2∠EAD＝90°，AG＝1，AB＝5，求线段CD的长．

Answer 1

【答案】（1）证明见解析；（2）CD=4．

【解析】

（1）由余角的性质可得结论；

（2）如图，过点A作AH⊥CD，延长BF交AH于M，可证四边形ABCH是正方形，可得AB＝CH＝5，由“ASA”可证△ABM≌△AHD，△AGF≌△AMF，可得HD＝AM，AM＝AG＝1，即可求解．

证明：（1）∵BF⊥AD，

∴∠AFB＝90°，

∴∠DAB+∠ABF＝90°，

∵∠ABC＝90°，即∠ABF+∠FBC＝90°，

∴∠DAB＝∠FBC；

（2）如图，过点A作AH⊥CD，垂足为H，延长BF交AH于M，

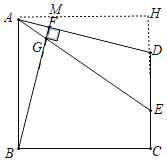
∵AH⊥CD，∠ABC＝∠DCB＝90°，

∴四边形ABCH是矩形，

又∵AB＝BC，

∴矩形ABCH是正方形，

∴AB＝CH＝5，

∵∠BAE+2∠EAD＝90°，∠BAE+∠EAD+∠DAH＝90°，∠BAE+∠DAE+∠ABM＝90°

∴∠DAH＝∠EAD＝∠ABM，

又AB＝AH，∠BAM＝∠H＝90°，

∴△ABM≌△HAD（ASA）

∴HD＝AM，

∵∠DAE＝∠DAH，AF＝AF，∠AFG＝∠AFM＝90°，

∴△AGF≌△AMF（ASA）

∴AM＝AG＝1，

∴HD＝1，

∴CD＝CH﹣DH＝4．