题目内容
【题目】如图,在平面直角坐标系中,点A(![]() ,0),AB⊥
,0),AB⊥![]() 轴,且AB=10,点C(0,b),
轴,且AB=10,点C(0,b),![]() ,b满足
,b满足![]() .点P(t,0)是线段AO上一点(不包含A,O)
.点P(t,0)是线段AO上一点(不包含A,O)
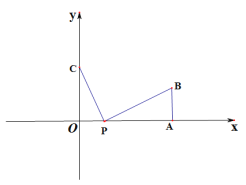
(1)当t=5时,求PB:PC的值;
(2)当PC+PB最小时,求t的值;
(3)请根据以上的启发,解决如下问题:正数m,n满足m+n=10,且正数![]() =
=![]() ,则正数
,则正数![]() 的最小值=________.
的最小值=________.
【答案】(1)![]() 的值为
的值为![]() ;(2)当
;(2)当![]() 最小时,t的值为15;(3)
最小时,t的值为15;(3)![]() .
.
【解析】
(1)先根据二次根式的被开方数的非负性求出a、b的值,从而可得OA、OC的长,再利用勾股定理分别求出PB、PC的长,从而可得出答案;
(2)如图(见解析),作点B关于x轴的对称点![]() ,从而可得
,从而可得![]() 的长,再根据两点之间线段最短确认
的长,再根据两点之间线段最短确认![]() 最小时点P的位置,然后根据等腰直角三角形的性质求解即可得;
最小时点P的位置,然后根据等腰直角三角形的性质求解即可得;
(3)先根据题(1)得出![]() 的式子,可发现与所求的
的式子,可发现与所求的![]() 的形式完全一样,因此,参照题(2)的方法,画出图形,利用几何方法求解即可(与题(2)的思路完全相同).
的形式完全一样,因此,参照题(2)的方法,画出图形,利用几何方法求解即可(与题(2)的思路完全相同).
![]()
![]() ,解得
,解得![]()
将![]() 代入得,
代入得,![]()
![]()
![]()
(1)当![]() 时,则
时,则![]()
![]() 轴
轴
![]()
![]()
![]()
故![]() 的值为
的值为![]() ;
;
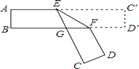
(2)如图1,作点B关于x轴的对称点![]() ,过点
,过点![]() 作
作![]() 轴于点D,连接
轴于点D,连接![]() ,
,![]() 交x轴于点
交x轴于点![]()
由轴对称的性质得:![]()
![]()
由两点之间线段最短得:当点P与点![]() 重合时,
重合时,![]() 最小,最小值为
最小,最小值为![]()
![]()
![]()
![]() 是等腰直角三角形,
是等腰直角三角形,![]()
![]() 是等腰直角三角形,
是等腰直角三角形,![]()
![]()
故当![]() 最小时,t的值为15;
最小时,t的值为15;
(3)由(1)知,![]()
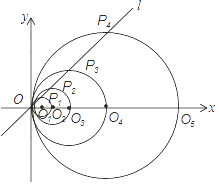
因此,对于![]() 可参照(2)的方法,画出如图2,其中,点B与点
可参照(2)的方法,画出如图2,其中,点B与点![]() 关于x轴对称,
关于x轴对称,![]() 轴,
轴,![]()
则![]()
由(2)可知,![]() 的最小值为
的最小值为![]()
![]()
![]()
即![]() 的最小值为
的最小值为![]()
故答案为:![]() .
.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目