题目内容
4.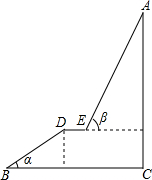 如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车到达A处,返程时从A处乘坐升降电梯直接到达C处,已知:AC⊥BC于C,DE∥BC,BC=110米,DE=9米,BD=60米,α=32°,β=68°,求AC的高度.(参考数据:sin32°≈0.53;cos32°≈0.85;tan32°≈0.62;sin68°≈0.93;cos68°≈0.37;tan68°≈2.48)
如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车到达A处,返程时从A处乘坐升降电梯直接到达C处,已知:AC⊥BC于C,DE∥BC,BC=110米,DE=9米,BD=60米,α=32°,β=68°,求AC的高度.(参考数据:sin32°≈0.53;cos32°≈0.85;tan32°≈0.62;sin68°≈0.93;cos68°≈0.37;tan68°≈2.48)
分析 根据已知和余弦的概念求出DF的长,得到CG的长,根据正切的概念求出AG的长,求和得到答案.
解答 解:∵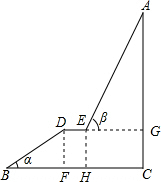 cos∠DBF=$\frac{BF}{BD}$,
cos∠DBF=$\frac{BF}{BD}$,
∴BF=60×0.85=51,
FH=DE=9,
∴EG=HC=110-51-9=50,
∵tan∠AEG=$\frac{AG}{EG}$,
∴AG=50×2.48=124,
∵sin∠DBF=$\frac{DF}{BD}$,
∴DF=60×0.53=31.8,
∴CG=31.8,
∴AC=AG+CG=124+31.8=155.8米.
点评 本题考查的是解直角三角形的应用,掌握锐角三角函数的概念和坡角的概念是解题的关键,解答时注意:正确作出辅助线构造直角三角形准确运用锐角三角函数的概念列出算式.

练习册系列答案
相关题目
9.直角三角形的两边长分别为3和5,则另一边长为( )
| A. | 4 | B. | $\sqrt{41}$ | C. | 4或$\sqrt{34}$ | D. | 4或$\sqrt{41}$ |
 如图,在四边形ABCD中,AD∥BC,∠ABC=90°,E为AD上一点,将△ABE沿直线BE折叠,使点A落在BD上的点G处,延长EG交BC于点F.
如图,在四边形ABCD中,AD∥BC,∠ABC=90°,E为AD上一点,将△ABE沿直线BE折叠,使点A落在BD上的点G处,延长EG交BC于点F.
 如图所示,有一条宽度相等的小路穿过矩形草地ABCD,若AB=60m,BC=81m,AE=100m,则这条小路的面积是多少?
如图所示,有一条宽度相等的小路穿过矩形草地ABCD,若AB=60m,BC=81m,AE=100m,则这条小路的面积是多少?