题目内容
14.已知四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,∠DAB=45°.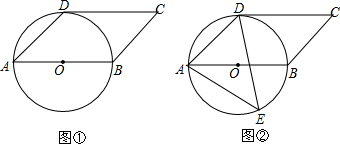
(Ⅰ)如图①,判断CD与⊙O的位置关系,并说明理由;
(Ⅱ)如图②,E是⊙O上一点,且点E在AB的下方,若⊙O的半径为3cm,AE=5cm,求点E到AB的距离.
分析 (1)连接OD,则∠AOD为直角,由四边形ABCD是平行四边形,则AB∥DC.从而得出∠CDO=90°,即可证出答案.
(2)作EF⊥AB于F,连接BE,根据圆周角定理得∠AEB=90°,然后根据勾股定理求得BE,然后根据sin∠BAE=$\frac{BE}{AB}$=$\frac{EF}{AE}$求得EF即可.
解答 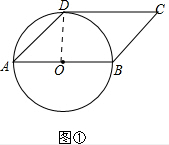 解:(1)CD与圆O相切.
解:(1)CD与圆O相切.
证明:如图①,连接OD,则∠AOD=2∠DAB=2×45°=90°,
∵四边形ABCD是平行四边形,
∴AB∥DC.
∴∠CDO=∠AOD=90°.
∴OD⊥CD.
∴CD与圆O相切.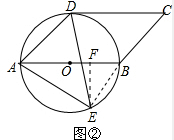
(2)如图②,作EF⊥AB于F,连接BE,
∵AB是圆O的直径,
∴∠AEB=90°,AB=2×3=6.
∵AE=5,
∴BE=$\sqrt{A{B}^{2}-A{E}^{2}}$=$\sqrt{11}$,
∵sin∠BAE=$\frac{BE}{AB}$=$\frac{EF}{AE}$.
∴$\frac{\sqrt{11}}{6}$=$\frac{EF}{5}$
∴EF=$\frac{5\sqrt{11}}{6}$.
点评 本题考查了切线的判定和性质、平行四边形的性质以及圆周角定理,注意辅助线的作法是解此题的关键.

练习册系列答案
相关题目
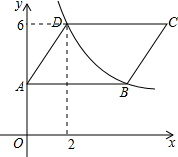 如图,平行四边形ABCD的顶点B,D都在反比例函数y=$\frac{k}{x}$(x>0)的图象上,点D的坐标为(2,6),AB平行于x轴,点A的坐标为(0,3),将这个平行四边形像左平移2个单位,再向下平移3个单位后,点C的坐标为( )
如图,平行四边形ABCD的顶点B,D都在反比例函数y=$\frac{k}{x}$(x>0)的图象上,点D的坐标为(2,6),AB平行于x轴,点A的坐标为(0,3),将这个平行四边形像左平移2个单位,再向下平移3个单位后,点C的坐标为( )



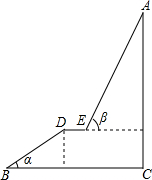 如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车到达A处,返程时从A处乘坐升降电梯直接到达C处,已知:AC⊥BC于C,DE∥BC,BC=110米,DE=9米,BD=60米,α=32°,β=68°,求AC的高度.(参考数据:sin32°≈0.53;cos32°≈0.85;tan32°≈0.62;sin68°≈0.93;cos68°≈0.37;tan68°≈2.48)
如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车到达A处,返程时从A处乘坐升降电梯直接到达C处,已知:AC⊥BC于C,DE∥BC,BC=110米,DE=9米,BD=60米,α=32°,β=68°,求AC的高度.(参考数据:sin32°≈0.53;cos32°≈0.85;tan32°≈0.62;sin68°≈0.93;cos68°≈0.37;tan68°≈2.48)