��Ŀ����
����Ŀ��ij�����Ǿ���A�ͺŲʵ磬�������·�ÿ̨�ʵ��ۼ���ȥ��ͬ����Ƚ���500Ԫ����������ʵ��������ͬ����ȥ�����۶�Ϊ5��Ԫ���������۶�Ϊ4��Ԫ��
��1����ȥ�����·�ÿ̨A�ͺŲʵ��ۼ��Ƕ���Ԫ��
��2��Ϊ�˸��ƾ�Ӫ�������Ǿ����پ���B�ͺŲʵ磮��֪A�ͺŲʵ�ÿ̨������Ϊ1800Ԫ��B�ͺŲʵ�ÿ̨������Ϊ1500Ԫ��������Ԥ���ò�����3.3��Ԫ�Ҳ�����3.2��Ԫ���ʽ������ֲʵ繲20̨�������ļ��ֽ���������
��3������������A�ͺŲʵ������ԭ�۳��ۣ�B�ͺŲʵ���ÿ̨1800Ԫ�ļ۸���ۣ��������ʵ�ȫ��������ǰ���£���ν�������ʹ�����ǻ��������������Ƕ��٣�
���𰸡���1��ȥ�����·�ÿ̨A�ͺŲʵ��ۼ���2500Ԫ����2����4�ֽ�������������һ������A���ͺŵIJʵ�7̨��B���ͺŲʵ�13̨��������������A���ͺŵIJʵ�8̨��B���ͺŲʵ�12̨��������������A���ͺŵIJʵ�9̨��B���ͺŲʵ�11̨�������ģ�����A���ͺŵIJʵ�10̨��B���ͺŲʵ�10̨����3���������ʵ�ȫ��������ǰ���£�����A���ͺŵIJʵ�7̨��B���ͺŲʵ�13̨����ʹ�����ǻ���������������5300Ԫ��
��������
��1��������ȥ�����·�ÿ̨A�ͺŲʵ��ۼ���xԪ���ٸ���ȥ�����������������ͬ�г����̣����ɵý⣻
��2������������ǹ���A���ͺŵIJʵ�ą���ٸ��������г�һԪһ�β���ʽ�飬��ü��ɣ�
��3��������������ΪwԪ���ٸ��������г�һ�κ����������ж���a��7ʱ��wȡ�����ֵ����ʱw��5300�����ɵý�.
�⣺��1����ȥ�����·�ÿ̨A�ͺŲʵ��ۼ���xԪ��
![]() ��
��
��ã�x��2500��
�����飬x��2500��ԭ��ʽ���̵Ľ⣬
��ȥ�����·�ÿ̨A�ͺŲʵ��ۼ���2500Ԫ��
��2��������ǹ���A���ͺŵIJʵ�ą��
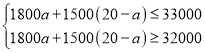 ��
��
��ã�![]() ��a��10��
��a��10��
��a������
��a��7��8��9��10��
������4�ֽ���������
����һ������A���ͺŵIJʵ�7̨��B���ͺŲʵ�13̨��
������������A���ͺŵIJʵ�8̨��B���ͺŲʵ�12̨��
������������A���ͺŵIJʵ�9̨��B���ͺŲʵ�11̨��
�����ģ�����A���ͺŵIJʵ�10̨��B���ͺŲʵ�10̨��
��3����������ΪwԪ��
w����2500��500��1800��a+��1800��1500����20��a������100a+6000��
��a��7��8��9��10��
�൱a��7ʱ��wȡ�����ֵ����ʱw��5300��
���������ʵ�ȫ��������ǰ���£�����A���ͺŵIJʵ�7̨��B���ͺŲʵ�13̨����ʹ�����ǻ���������������5300Ԫ��