题目内容
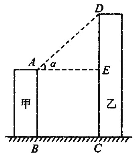
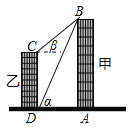
【题目】如图,线段AB、CD分别表示甲乙两建筑物的高,BA⊥AD,CD⊥DA,垂足分别为A、D.从D点测到B点的仰角α为60°,从C点测得B点的仰角β为30°,甲建筑物的高AB=30米
(1)求甲、乙两建筑物之间的距离AD.
(2)求乙建筑物的高CD.
【答案】(1)![]() ;(2)20.
;(2)20.
【解析】
(1)在Rt△ABD中利用三角函数即可求解;
(2)作CE⊥AB于点E,在Rt△BCE中利用三角函数求得BE的长,然后根据CD=AE=AB﹣BE求解.
(1)作CE⊥AB于点E,在Rt△ABD中,AD=![]() =
=![]() =
=![]() (米);
(米);
(2)在Rt△BCE中,CE=AD=![]() 米,BE=CEtanβ=
米,BE=CEtanβ=![]() ×
×![]() =10(米),则CD=AE=AB﹣BE=30﹣10=20(米)
=10(米),则CD=AE=AB﹣BE=30﹣10=20(米)
答:乙建筑物的高度DC为20m.


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某射击队要从甲、乙、丙、丁四人中选拔一名选手参赛,在选拔赛中,每人射击10次,然后从他们的成绩平均数(环)及方差两个因素进行分析,甲、乙、丙的成绩分析如表所示,丁的成绩如图所示.
甲 | 乙 | 丙 | |
平均数 | 7.9 | 7.9 | 8.0 |
方差 | 3.29 | 0.49 | 1.8 |
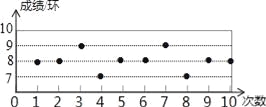
根据以上图表信息,参赛选手应选( )
A. 甲 B. 乙 C. 丙 D. 丁