题目内容
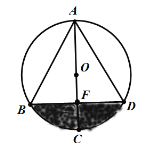
【题目】如图,已知在⊙O中,AB=4![]() , AF=6,AC是直径,AC⊥BD于F,图中阴影部分的面积是( )
, AF=6,AC是直径,AC⊥BD于F,图中阴影部分的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
利用勾股定理求得BD=2BF=4![]() ,连接OB、OD、BC,先求得∠ABC=90°,进而根据射影定理求得FC=2,从而求得直径的长,根据余弦函数求得∠BAF=30°,进而得出∠BOD=120°,最后根据S阴影=S扇形-S△BOD即可求得阴影的面积.
,连接OB、OD、BC,先求得∠ABC=90°,进而根据射影定理求得FC=2,从而求得直径的长,根据余弦函数求得∠BAF=30°,进而得出∠BOD=120°,最后根据S阴影=S扇形-S△BOD即可求得阴影的面积.
解:∵AC是直径,AC⊥BD于F,
∴BF=DF,![]() ,
,
∴∠BAC=∠DAC,
在RT△ABF中, ![]()
∴BD=2BF=4![]() ,
,
连接OB、OD、BC,
∵AC是直径,
∴∠ABC=90°,
∴BF2=AFFC,即(2![]() )2=6FC,
)2=6FC,
∴FC=2,
∴直径AC=AF+FC=6+2=8,
∴⊙O的半径为4,
∵AB=4![]() ,AF=6,
,AF=6,
∴![]() ,
,
∴∠BAF=30°,
∴∠BAD=60°,
∴∠BOD=120°,
∵OC=4,FC=2,
∴OF=2,
∴![]()
![]()
故选择:D.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某射击队要从甲、乙、丙、丁四人中选拔一名选手参赛,在选拔赛中,每人射击10次,然后从他们的成绩平均数(环)及方差两个因素进行分析,甲、乙、丙的成绩分析如表所示,丁的成绩如图所示.
甲 | 乙 | 丙 | |
平均数 | 7.9 | 7.9 | 8.0 |
方差 | 3.29 | 0.49 | 1.8 |
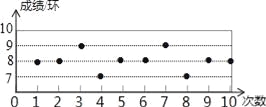
根据以上图表信息,参赛选手应选( )
A. 甲 B. 乙 C. 丙 D. 丁