题目内容
13.有这样一组数据a1,a2,a3,…an,满足以下规律:a1=$\frac{1}{2}$,a2=$\frac{1}{1-{a}_{1}}$,a3=$\frac{1}{1-{a}_{2}}$,…,an=$\frac{1}{1-{a}_{n-1}}$(n≥2且n为正整数),则a2017的值为$\frac{1}{2}$(结果用数字表示)
分析 求出数列的前4项,继而得出数列的循环周期,然后求解可得.
解答 解:∵a1=$\frac{1}{2}$,
a2=$\frac{1}{1-{a}_{1}}$=$\frac{1}{1-\frac{1}{2}}$=2,
a3=$\frac{1}{1-{a}_{2}}$=$\frac{1}{1-2}$=-1,
a4=$\frac{1}{1-{a}_{3}}$=$\frac{1}{1-(-1)}$=$\frac{1}{2}$,
…
∴这列数每3个数为一周期循环,
∵2017÷3=672…1,
∴a2017=a1=$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题主要考查数字的变化规律,解决此类问题时通常需要确定数列与序数的关系或者数列的循环周期等,此题得出这列数每3个数为一周期循环是解题的关键.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
18.下列图形是四种运动品牌的商标,其中是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
5.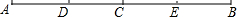 如图,C是AB的中点,D、E分别是AC、BC的中点,下列结论错误的是( )
如图,C是AB的中点,D、E分别是AC、BC的中点,下列结论错误的是( )
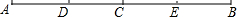 如图,C是AB的中点,D、E分别是AC、BC的中点,下列结论错误的是( )
如图,C是AB的中点,D、E分别是AC、BC的中点,下列结论错误的是( )| A. | AC=2CE | B. | AB-AD=2CD | C. | AD=$\frac{1}{3}$DB | D. | DE=$\frac{1}{2}$AB |
3.-5的相反数是( )
| A. | $\frac{1}{5}$ | B. | -$\frac{1}{5}$ | C. | 5 | D. | -5 |
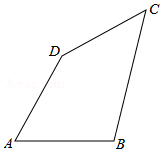 如图,在四边形ABCD中,AB=AD=8,∠A=60°,BC=10,CD=6.
如图,在四边形ABCD中,AB=AD=8,∠A=60°,BC=10,CD=6.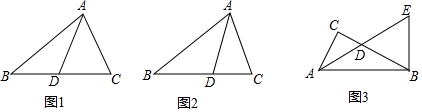
 如图,已知∠ACD是△ABC的一个外角,∠ACD=130°,∠B=70°,则∠A的度数为60°.
如图,已知∠ACD是△ABC的一个外角,∠ACD=130°,∠B=70°,则∠A的度数为60°.