题目内容
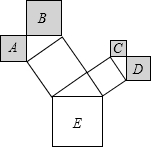如图，是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形．若最大正方形E的面积为100，则A、B、C、D四个正方形的面积之和为
考点：勾股定理
专题：
分析：根据正方形的面积公式，结合勾股定理，能够导出正方形A，B，C，D的面积和即为最大正方形的面积．
解答：
解：根据勾股定理的几何意义，可得A、B的面积和为S1，C、D的面积和为S2，S1+S2=S3，于是S3=S1+S2，
即S3=A+B+C+D=100．
故答案为：100．
解：根据勾股定理的几何意义，可得A、B的面积和为S1，C、D的面积和为S2，S1+S2=S3，于是S3=S1+S2，即S3=A+B+C+D=100．
故答案为：100．
点评：本题考查了勾股定理的应用．能够发现正方形A，B，C，D的边长正好是两个直角三角形的四条直角边，根据勾股定理最终能够证明正方形A，B，C，D的面积和即是最大正方形的面积．
练习册系列答案
阅读快车系列答案
相关题目
当∠1，∠2，∠3满足条件
如图，a，b，c为实数，则|a-c|-| (b-a)2 |
| A、-2b | B、-2c |
| C、-2a+2b | D、0 |
已知x2+kx+16是完全平方式，则常数k等于（ ）
| A、±4 | B、±8 | C、4 | D、8 |
已知△ABC在平面直角坐标系中的位置如图所示，将△ABC先向下平移5个单位，再向左平移2个单位，求平移后C点的坐标和△ABC所扫过部分的面积．
如图，点E是AB，CD外一点，且AB∥CD，∠BED，∠B，∠D又有何关系，并加以说明．下列四个图案中，是轴对称图形的个数是（ ）
| A、1 | B、2 | C、3 | D、4 |
如图，四边形ABCD是菱形，且∠A=60°，又E，F，G，H分别是菱形各边的中点，联结EH，FG，请判断六边形EBFGDH是一个怎样的图形？并说明你的结论．