题目内容
17.平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(-1,0),点C在y轴上,如果三角形ABC的面积等于6,则点C的坐标为(0,4)或(0,-4).分析 先求出AB的长度,再根据三角形的面积求出点C的纵坐标,然后根据y轴上点的坐标特征写出即可.
解答 解:∵点A的坐标为(2,0),点B的坐标为(-1,0),
∴A、B都在x轴上,且AB=2-(-1)=3,
设点C的纵坐标为y,
∵△ABC的面积等于6,
∴$\frac{1}{2}$×3×|y|=6,
解得y=±4,
∵点C在y轴上,
∴点C的坐标为(0,4)或(0,-4).
故答案为:(0,4)或(0,-4).
点评 本题考查了坐标与图形性质,三角形的面积,易错点在于要注意点C有两种情况.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.B题:图①~④分别表示甲、乙两辆汽车在同一条路上匀速行驶中速度与时间的关系,小明对4个图中汽车运动的情况进行了描述,其中正确的是( )


| A. | 图①:乙的速度是甲的2倍,甲乙的路程相等 | |
| B. | 图②:乙的速度是甲的2倍,甲的路程是乙的一半 | |
| C. | 图③:乙的速度是甲的2倍,乙的路程是甲的一半 | |
| D. | 图④:甲的速度是乙的2倍,甲乙的路程相等 |
12.$\sqrt{9}$的值是( )
| A. | ±3 | B. | -3 | C. | 3 | D. | 81 |
2.下列分式从左到右边形正确的是( )
| A. | $\frac{b}{a}=\frac{b+1}{a+1}$ | B. | $\frac{b}{a}=\frac{b(m+1)}{a(m+1)}$ | C. | $\frac{bm}{am}=\frac{b}{a}$ | D. | $\frac{a+b}{ab}=\frac{b+1}{b}$ |
 如图,直线c与直线a、b相交,且a∥b,则结论:
如图,直线c与直线a、b相交,且a∥b,则结论: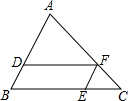 如图,在△ABC中,点D,F,E分别在边AB,AC,BC上,且DF∥BC,EF∥AB,若AD=2BD,则$\frac{CE}{BE}$的值为$\frac{1}{2}$.
如图,在△ABC中,点D,F,E分别在边AB,AC,BC上,且DF∥BC,EF∥AB,若AD=2BD,则$\frac{CE}{BE}$的值为$\frac{1}{2}$.