题目内容
16.如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作FE⊥AB于点E,交AC的延长线于点F.(1)求证:EF与⊙O相切;

(2)若⊙O的半径为5,DE=4,求EB的长.
分析 (1)连结AD、OD,如图,根据圆周角定理由AB为⊙O的直径得到∠ADB=90°,即AD⊥BC,再根据等腰三角形的性质得BD=CD,则OD为△ABC的中位线,所以OD∥AB,加上EF⊥AC,于是OD⊥EF,然后根据切线的判定定理得EF是⊙O的切线;
(2)先由OD∥AC,得到OF与FD的关系,根据勾股定理求出DF,OF,再用OD∥AE,得出$\frac{OD}{AE}=\frac{OF}{AF}$,求出即可.
解答 解:(1)证明:连结AD、OD,如图,
∵AB为⊙O的直径,
∴∠ADB=90°,即AD⊥BC,
∵AB=AC,
∴BD=CD,
∵OA=OC,
∴OD为△ABC的中位线,
∴OD∥AB,
∵EF⊥AC,
∴OD⊥EF,
∴EF是⊙O的切线;
(2)连接OD,AD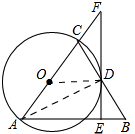
∵OD∥AE,
∴$\frac{OF}{OA}=\frac{FD}{DE}$,
即$\frac{OF}{5}=\frac{FD}{4}$,
设OF=5x,FD=4x,
在Rt△ODF中,OD=5,
∴OF2=FD2+25,
∴25x2=16x2+25,
∴x=$\frac{5}{3}$或x=-$\frac{5}{3}$(舍),
∴OF=$\frac{25}{3}$,FD=$\frac{20}{3}$,
∵OD∥AE,
∴$\frac{OD}{AE}=\frac{OF}{AF}$,
∴$\frac{5}{AE}=\frac{\frac{25}{3}}{5+\frac{25}{3}}$,
∴AE=8,
∴EB=AB-AE=AC-AE=10-8=2
点评 本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了圆周角定理和相似三角形的判定与性质.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
7.如图,把边长为(a+2)的正方形纸片剪出一个边长为a的正方形之后,剩余部分又剪拼成一个长方形(不重叠无缝隙),若拼成的长方形一边长为2,则长方形的面积是( )


| A. | 2(2a+2) | B. | 2a+4 | C. | 4a+8 | D. | 2(a+4) |
1. 如图,在四边形ABCD中,AC与BD交于点M,若∠ADM=40°,∠AMD=90°,AB=AC=AD,则∠ABC的度数为( )
如图,在四边形ABCD中,AC与BD交于点M,若∠ADM=40°,∠AMD=90°,AB=AC=AD,则∠ABC的度数为( )
 如图,在四边形ABCD中,AC与BD交于点M,若∠ADM=40°,∠AMD=90°,AB=AC=AD,则∠ABC的度数为( )
如图,在四边形ABCD中,AC与BD交于点M,若∠ADM=40°,∠AMD=90°,AB=AC=AD,则∠ABC的度数为( )| A. | 55° | B. | 60° | C. | 65° | D. | 75° |
5.下列语句正确的是( )
| A. | 有一个角对应相等的两个直角三角形相似 | |
| B. | 如果两个图形位似,那么对应线段平行或在同一条直线直线上 | |
| C. | 两个矩形一定相似 | |
| D. | 如果将一个三角形的各边长都扩大二倍,则其面积将扩大4倍 |
 如图,已知两条射线PQ∥MN,线段AB的两个端点A、B分别在射线PQ、MN上,且∠M=∠ABM=72°,D在线段MB上(点D不与M、B重合),PB平分∠APD,PC平分∠MPD.
如图,已知两条射线PQ∥MN,线段AB的两个端点A、B分别在射线PQ、MN上,且∠M=∠ABM=72°,D在线段MB上(点D不与M、B重合),PB平分∠APD,PC平分∠MPD.
 如图,在平面直角坐标系xOy中,A(2,0),B(2,4),C(0,4).若直线y=kx-2k+1(k是常数)将四边形OABC分成面积相等的两部分,则k的值为-1.
如图,在平面直角坐标系xOy中,A(2,0),B(2,4),C(0,4).若直线y=kx-2k+1(k是常数)将四边形OABC分成面积相等的两部分,则k的值为-1.