Question

10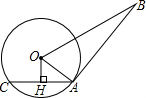．如图，AB是⊙O的切线，A为切点，AC是⊙O的弦，过点O作OH⊥AC于H．若OH=3，AB=12，BO=13．则弦AC的长为8．

Answer 1

分析 首先根据切线的性质可得∠OAB=90°，利用勾股定理计算出AO的长，再利用勾股定理计算出AH的长，根据垂径定理可得AC=2AH，进而可得答案．

解答 解：∵AB是⊙O的切线，A为切点，
∴∠OAB=90°，
∵AB=12，BO=13，
∴AO=$\sqrt{O{B}^{2}-A{B}^{2}}$=$\sqrt{1{3}^{2}-1{2}^{2}}$=5，
∵OH⊥AC，
∴AC=2AH，
∵OH=3，
∴AH=$\sqrt{A{O}^{2}-H{O}^{2}}$=4，
∴AC=8，
故答案为：8．

点评 此题主要考查了切线的性质、垂径定理和勾股定理，关键是掌握圆的切线垂直于经过切点的半径，垂直弦的直径平分这条弦，并且平分弦所对的两条弧．