题目内容
19.分式$\frac{x+y}{{{x^2}y}}$中的x、y都扩大为原来的10倍,则分式的值( )| A. | 不变 | B. | 扩大为原来的10倍 | ||
| C. | 缩小为原来的$\frac{1}{100}$ | D. | 缩小到原来的$\frac{1}{10}$ |
分析 直接利用分式的基本性质化简得出答案.
解答 解:∵分式$\frac{x+y}{{{x^2}y}}$中的x、y都扩大为原来的10倍,
∴$\frac{10x+10y}{(10x)^{2}×10y}$=$\frac{x+y}{100{x}^{2}y}$=$\frac{1}{100}$×$\frac{x+y}{{x}^{2}y}$,即分式的值缩小为原来的$\frac{1}{100}$.
故选:C.
点评 此题主要考查了分式的基本性质,正确掌握分式的性质是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.下列说法正确的是( )
| A. | 4的算术平方根是$\sqrt{2}$ | B. | 27的立方根是±3 | ||
| C. | $\sqrt{16}$的平方根是±2 | D. | $\sqrt{9}$的平方根是±3 |
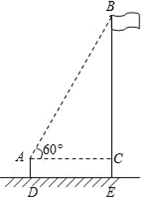 某校初三(一)班课外活动小组为了测得学校旗杆的高度,它们在离旗杆6米的A处,用高为1.5米的仪器测得旗杆顶部B处的仰角为60°,如图所示,则旗杆的高度为11.9米.(已知$\sqrt{3}$≈1.732结果精确到0.1米)
某校初三(一)班课外活动小组为了测得学校旗杆的高度,它们在离旗杆6米的A处,用高为1.5米的仪器测得旗杆顶部B处的仰角为60°,如图所示,则旗杆的高度为11.9米.(已知$\sqrt{3}$≈1.732结果精确到0.1米)