题目内容
9.已知直线AB上有一点C,AB>BC,BC=4cm,M是AB的中点,N是AC的中点,求MN的长.分析 分类讨论:C在线段AB上,C在线段AB的延长线上,根据线段中点的性质,可得MA、AN的长,根据线段的和差,可得答案.
解答 解:①C在线段AB的延长线上,由线段中点的性质,得MA=$\frac{1}{2}$AB,AN=$\frac{1}{2}$AC=$\frac{1}{2}$(AB+BC),
由线段的和差,得MN=$\frac{1}{2}$(AB+BC)-$\frac{1}{2}$AB=$\frac{1}{2}$BC=2,
②C在线段AB上,由线段中点的性质,得AM=$\frac{1}{2}$AB,AN=$\frac{1}{2}$AC=$\frac{1}{2}$(AB-BC),
由线段的和差,得MN=AM-AN=$\frac{1}{2}$BC=2.
点评 本题考查了两点间的距离,分类讨论是解题关键,利用了线段的和差,线段中点的性质.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
17.如果将抛物线y=2x2向上平移1个单位,那么所得的抛物线的解析式是( )
| A. | y=2(x-1)2 | B. | y=2(x+1)2 | C. | y=2x2-1 | D. | y=2x2+1 |
4.永登县明天降雪的概率是30%,对此消息下列说法中中正确的是( )
| A. | 永登县明天将有30%的地区降雪 | B. | 永登县明天将有30%的时间降雪 | ||
| C. | 永登县明天降雪的可能性较小 | D. | 永登县明天肯定不降雪 |
14. 如图,AB是⊙O的直径,弦CD⊥AB于E,若OA=2,∠B=60°,则CD的长( )
如图,AB是⊙O的直径,弦CD⊥AB于E,若OA=2,∠B=60°,则CD的长( )
 如图,AB是⊙O的直径,弦CD⊥AB于E,若OA=2,∠B=60°,则CD的长( )
如图,AB是⊙O的直径,弦CD⊥AB于E,若OA=2,∠B=60°,则CD的长( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2$\sqrt{5}$ | D. | 4 |
1.已知:x-2y=-3,则5(x-2y)2-3(x-2y)+40的值是( )
| A. | 5 | B. | 94 | C. | 45 | D. | -4 |
18.-1$\frac{1}{3}$的倒数是( )
| A. | -$\frac{4}{3}$ | B. | $\frac{4}{3}$ | C. | -$\frac{3}{4}$ | D. | $\frac{3}{4}$ |
19.下面的几何体中,属于棱柱的有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,一次函数y=-2x+4的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°,求:
如图,一次函数y=-2x+4的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°,求: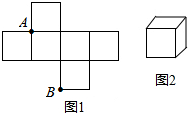 图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,则在图2中,小虫从点A沿着正方体的棱长爬行到点B的长度为( )
图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,则在图2中,小虫从点A沿着正方体的棱长爬行到点B的长度为( )