题目内容
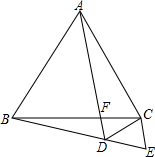 等边△ABC中,F为边BC边上的点,作∠CBE=∠CAF,延长AF与BE交于点D,截取BE=AD,连接CE.
等边△ABC中,F为边BC边上的点,作∠CBE=∠CAF,延长AF与BE交于点D,截取BE=AD,连接CE.(1)求证:CE=CD;
(2)求证:DC平分∠ADE;
(3)试判断△CDE的形状,并说明理由.
考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:
分析:(1)证明△ADC≌△BEC,然后根据全等三角形的对应边相等即可证得;
(2)根据ADC≌△BEC,可证得∠ADC=∠E,CE=CD,然后根据等边对等角即可证得;
(3)根据△ADC≌△BEC,证得∠ACD=∠BCE,得到∠DCE=∠ACB=60°,然后根据有一个角是60度的等腰三角形是等边三角形,即可证得.
(2)根据ADC≌△BEC,可证得∠ADC=∠E,CE=CD,然后根据等边对等角即可证得;
(3)根据△ADC≌△BEC,证得∠ACD=∠BCE,得到∠DCE=∠ACB=60°,然后根据有一个角是60度的等腰三角形是等边三角形,即可证得.
解答:解:(1)在△ADC和△BEC中,
,
∴△ADC≌△BEC(SAS),
∴CE=CD;
(2)∵△ADC≌△BEC,
∴∠ADC=∠E,CE=CD,
∵CE=CD,
∴∠CDE=∠E,
∴∠ADC=∠CDE,
∴DC平分∠ADE;
(3)△DCE为等边三角形.
∵△ADC≌△BEC,
∴∠ACD=∠BCE.
∴∠DCE=∠ACB=60°,
又∵CE=CD,
∴△DCE为等边三角形.
|
∴△ADC≌△BEC(SAS),
∴CE=CD;
(2)∵△ADC≌△BEC,
∴∠ADC=∠E,CE=CD,
∵CE=CD,
∴∠CDE=∠E,

∴∠ADC=∠CDE,
∴DC平分∠ADE;
(3)△DCE为等边三角形.
∵△ADC≌△BEC,
∴∠ACD=∠BCE.
∴∠DCE=∠ACB=60°,
又∵CE=CD,
∴△DCE为等边三角形.
点评:本题考查了全等三角形的判定与性质,以及等边三角形的判定方法,正确证得∠DCE=∠ACB=60°,是关键.

练习册系列答案
相关题目
在Rt△ABC中,∠C=90°,AC=5,BC=12,则点C到AB的距离是( )
| A、13 | ||
| B、5 | ||
| C、6 | ||
D、
|
某种商品的进价为300元,出售标价为440元,后来由于该商品积压,商店准备打折销售,但要保证利润率为10%,则商店可打( )
| A、6折 | B、6.5折 |
| C、7.3折 | D、7.5折 |
 如图,在平面直角坐标系xOy中,一次函数y=ax+b的图象与反比例函数
如图,在平面直角坐标系xOy中,一次函数y=ax+b的图象与反比例函数



 如图,点P是⊙O的直径BA的延长线上一点,PC切⊙O于点C,若∠P=30°,PB=6,则PC等于
如图,点P是⊙O的直径BA的延长线上一点,PC切⊙O于点C,若∠P=30°,PB=6,则PC等于 如图,直线AB、CD、EF相交于点O,OG⊥CD,∠BOD=32°.
如图,直线AB、CD、EF相交于点O,OG⊥CD,∠BOD=32°. 如图是一个正方体,用一个平面去截这个正方体,截面形状不可能是选项中的
如图是一个正方体,用一个平面去截这个正方体,截面形状不可能是选项中的