题目内容
如图，点P是⊙O的直径BA的延长线上一点，PC切⊙O于点C，若∠P=30°，PB=6，则PC等于考点：切线的性质
专题：
分析：连接OC，求出∠PCO=90°，设⊙O的半径是R，根据30°角所对的直角边等于斜边的一半求得R=2，由勾股定理得出22+PC2=（6-2）2，求出即可．
解答：
解：连接OC，
∵PC切⊙O于C
∴∠OCP=90°，
设⊙O的半径是R，则OP=6-R，
∵∠P=30°，
由30°角所对的直角边等于斜边的一半得，6-R=2R，
解得：R=2，
由勾股定理得：22+PC2=（6-2）2，
解得PC=2
故答案为：2
．
解：连接OC，∵PC切⊙O于C
∴∠OCP=90°，
设⊙O的半径是R，则OP=6-R，
∵∠P=30°，
由30°角所对的直角边等于斜边的一半得，6-R=2R，
解得：R=2，
由勾股定理得：22+PC2=（6-2）2，
解得PC=2
| 3 |
故答案为：2
| 3 |
点评：本题主要考查了切线的性质和勾股定理的应用，解此题的关键是能根据题意求出△PCO式直角三角形．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，AB与CD相交于点O，CO=DO，添加下列四个条件中的一个，其中不能断定△ACO与△BDO全等的条件是（ ）| A、AO=BO |
| B、AC∥BD |
| C、∠A=∠B |
| D、AC=BD |
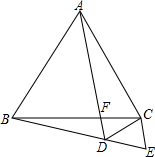等边△ABC中，F为边BC边上的点，作∠CBE=∠CAF，延长AF与BE交于点D，截取BE=AD，连接CE．
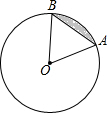如图，⊙O的半径为2，AB是⊙O的一条弦，∠O=60°，则图中阴影弓形的面积为已知线段a=2，b=4，线段c为a，b的比例中项，则c为（ ）
| A、3 | ||
B、±2
| ||
C、2
| ||
D、
|
下列几何体中，三视图既有圆又有长方形的是（ ）
| A、棱柱 | B、圆柱 | C、圆锥 | D、球 |