题目内容
 如图,直线AB、CD、EF相交于点O,OG⊥CD,∠BOD=32°.
如图,直线AB、CD、EF相交于点O,OG⊥CD,∠BOD=32°.(1)求∠AOG的度数;
(2)如果OC是∠AOE的平分线,那么OG是∠AOF的平分线吗?请说明理由.
考点:对顶角、邻补角,角平分线的定义,垂线
专题:
分析:(1)根据对顶角的性质,可得∠AOC的度数,根据角的和差,可得答案;
(2)根据角平分线的性质,可得∠AOC与∠COE的关系,根据对顶角的性质,可得∠DOF与∠COE的关系,根据等量代换,可得∠AOC与∠DOF的关系,根据余角的性质,可得答案.
(2)根据角平分线的性质,可得∠AOC与∠COE的关系,根据对顶角的性质,可得∠DOF与∠COE的关系,根据等量代换,可得∠AOC与∠DOF的关系,根据余角的性质,可得答案.
解答:解:(1)由对顶角相等,得∠AOC=∠BOD=32°,
由角的和差,得∠AOG=∠COG-∠AOC=90°-32°=58°;
(2)如果OC是∠AOE的平分线,那么OG是∠AOF的平分线,理由如下:
由OC是∠AOE的平分线,得∠COE=∠AOC=32°,
由对顶角相等,得∠DOF=∠COE,
等量代换,得∠DOF=∠AOC.
∠AOC+∠AOG=∠COG=90°,
∠DOF+∠FOG=∠DOG=90°,
由等角的余角相等,得∠AOG=∠FOG,
OG是∠AOF的平分线.
由角的和差,得∠AOG=∠COG-∠AOC=90°-32°=58°;
(2)如果OC是∠AOE的平分线,那么OG是∠AOF的平分线,理由如下:
由OC是∠AOE的平分线,得∠COE=∠AOC=32°,
由对顶角相等,得∠DOF=∠COE,
等量代换,得∠DOF=∠AOC.
∠AOC+∠AOG=∠COG=90°,
∠DOF+∠FOG=∠DOG=90°,
由等角的余角相等,得∠AOG=∠FOG,
OG是∠AOF的平分线.
点评:本题考查了对顶角、邻补角,(1)利用了对顶角相等的性质,角的和差;(2)利用了对顶角相等的性质,角的和差,还利用了余角的性质:等角的余角相等.

练习册系列答案
相关题目
已知线段a=2,b=4,线段c为a,b的比例中项,则c为( )
| A、3 | ||
B、±2
| ||
C、2
| ||
D、
|
下列几何体中,三视图既有圆又有长方形的是( )
| A、棱柱 | B、圆柱 | C、圆锥 | D、球 |
一件衬衫售价a元,利润为m%(m>0),则这种商品每件的成本是( )
A、
| ||
B、
| ||
| C、a(1+m%) | ||
| D、a(1-m%) |
 如图,在平面直角坐标系中,已知直线与x轴交于点A(-1,0),与y轴交于点C(0,-2).线段AC的中垂线交x轴于点B(
如图,在平面直角坐标系中,已知直线与x轴交于点A(-1,0),与y轴交于点C(0,-2).线段AC的中垂线交x轴于点B(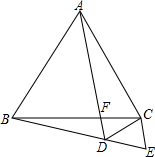 等边△ABC中,F为边BC边上的点,作∠CBE=∠CAF,延长AF与BE交于点D,截取BE=AD,连接CE.
等边△ABC中,F为边BC边上的点,作∠CBE=∠CAF,延长AF与BE交于点D,截取BE=AD,连接CE. 如图,过?ABCD的顶点C的直线交AB的延长线于点E,交AD的延长线于点F,若∠FCD=∠ECB,AF=8,则?ABCD的周长为
如图,过?ABCD的顶点C的直线交AB的延长线于点E,交AD的延长线于点F,若∠FCD=∠ECB,AF=8,则?ABCD的周长为