题目内容
在Rt△ABC中，∠C=90°，AC=5，BC=12，则点C到AB的距离是（ ）
| A、13 | ||
| B、5 | ||
| C、6 | ||
D、
|
考点：勾股定理
专题：
分析：首先利用勾股定理得出AB的长，进而利用三角形面积求出CD的长．
解答：
解：如图所示：过点C作CD⊥AB于点D，
∵在Rt△ABC中，∠C=90°，AC=5，BC=12，
∴AB=13，
∴
×AC×BC=
×CD×AB
∴5×12=13CD，
解得：CD=
．
故选：D．
解：如图所示：过点C作CD⊥AB于点D，∵在Rt△ABC中，∠C=90°，AC=5，BC=12，
∴AB=13，
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴5×12=13CD，
解得：CD=
| 60 |
| 13 |
故选：D．
点评：此题主要考查了勾股定理以及三角形面积，熟练利用三角形面积求出是解题关键．
练习册系列答案
期末100分闯关海淀考王系列答案
相关题目
如图，线段AB两个端点的坐标分别为A（4，4），B（6，2），以原点O为位似中心，在第一象限内将线段AB缩小为原来的| 1 |
| 2 |
| A、（2，2） |
| B、（2，1） |
| C、（3，2） |
| D、（3，1） |
如图，在平面直角坐标系中，已知直线与x轴交于点A（-1，0），与y轴交于点C（0，-2）．线段AC的中垂线交x轴于点B（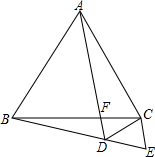
等边△ABC中，F为边BC边上的点，作∠CBE=∠CAF，延长AF与BE交于点D，截取BE=AD，连接CE．