题目内容
1.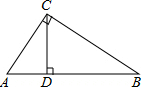 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.(1)求证:AC2=AD•AB;
(2)求证:AC2+BC2=AB2(即证明勾股定理);
(3)如果AC=4,BC=9,那么AD:DB的值是16:81;
(4)如果AD=4,DB=9,那么AC:BC的值是2:3.
分析 (1)欲证明AC2=AD•AB,只要证明△ACD∽△ABC.
(2)同理可证BC2=BD•AB,由AC2=AD•AB.推出AC2+BC2=AD•AB+BD•AB=AB2.
(3)由BC2=BD•AB,AC2=AD•AB,推出$\frac{AD•AB}{BD•AB}$=$\frac{A{C}^{2}}{B{C}^{2}}$,即$\frac{AD}{BD}$=$\frac{A{C}^{2}}{B{C}^{2}}$,由此即可计算.
(4)用类似(3)的方法计算即可.
解答 证明:(1)∵CD⊥AB,∠ACB=90°,
∴∠ADC=∠ACB=90°,
∵∠A=∠A,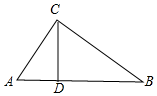
∴△ACD∽△ABC,
∴$\frac{AC}{AB}$=$\frac{AD}{AC}$,
∴AC2=AD•AB.
(2)同理可证BC2=BD•AB,
∵AC2=AD•AB.
∴AC2+BC2=AD•AB+BD•AB=AB2,
∴AC2+BC2=AB2.
(3)∵BC2=BD•AB,AC2=AD•AB,
∴$\frac{AD•AB}{BD•AB}$=$\frac{A{C}^{2}}{B{C}^{2}}$,
∴$\frac{AD}{BD}$=$\frac{A{C}^{2}}{B{C}^{2}}$=$\frac{16}{81}$.
故答案为16:81
(4)∵BC2=BD•AB,AC2=AD•AB,
∴$\frac{AD•AB}{BD•AB}$=$\frac{A{C}^{2}}{B{C}^{2}}$,
∴$\frac{A{C}^{2}}{B{C}^{2}}$=$\frac{AD}{DB}$=$\frac{4}{9}$,
∴$\frac{AC}{BC}$=$\frac{2}{3}$.
故答案为2:3.
点评 本题考查相似三角形的性质和判定、勾股定理等知识,解题的关键是灵活运用相似三角形的性质解决问题,学会利用结论解决问题.

| A. | 若a≠b,则a2≠b2 | B. | 若a2=b2,则a=b | ||
| C. | 若a>b,则a2>b2 | D. | 若a、b不全为零,则a2+b2>0 |
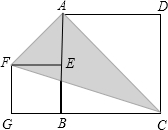 如图,正方形ABCD的边长为a,点E在AB边上,四边形EFGB也是正方形,它的边长为b(a>b),连结AF、CF、AC.
如图,正方形ABCD的边长为a,点E在AB边上,四边形EFGB也是正方形,它的边长为b(a>b),连结AF、CF、AC.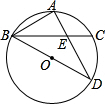 如图,BD为⊙O的直径,点A是弧BC的中点,AD交BC于E点,AE=2,ED=4
如图,BD为⊙O的直径,点A是弧BC的中点,AD交BC于E点,AE=2,ED=4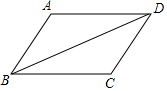 如图:请在下列四个条件:①AD∥BC,②AB=CD,③∠A=∠C,④AB∥CD中,选出两个,能推出△ABD≌△CDB:①②.(只要写出正确的一种即可)
如图:请在下列四个条件:①AD∥BC,②AB=CD,③∠A=∠C,④AB∥CD中,选出两个,能推出△ABD≌△CDB:①②.(只要写出正确的一种即可)