题目内容
16.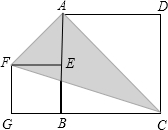 如图,正方形ABCD的边长为a,点E在AB边上,四边形EFGB也是正方形,它的边长为b(a>b),连结AF、CF、AC.
如图,正方形ABCD的边长为a,点E在AB边上,四边形EFGB也是正方形,它的边长为b(a>b),连结AF、CF、AC.(1)用含a、b的代数式表示AE=a-b;
(2)若a+b=10,ab=20,求这两个正方形的面积之和;
(3)若a=10,△AFC的面积为S,则点E从点A向点B滑动的过程中,S的值是否会发生改变?若会,请说明理由;若不会,请求出S.
分析 (1)根据题意可知:AE=AB-BE=a-b;
(2)根据完全平方公式即可求出答案.
(3)设CF与AB交于点H,分别求出AH、EF、BC的长度即可求出S的值.
解答 解:(1)AE=AB-BE=a-b
(2)∵(a+b)2=a2+2ab+b2,
∴这两个正方形的面积之和为:a2+b2=(a+b)2-2ab=100-40=60
(3) 设CF与AB交于H,
设CF与AB交于H,
∴BC=10,GB=GF=b,
∵BH∥GF,
∴△BCH∽△GCF
∴$\frac{BH}{GF}=\frac{BC}{CG}$,
∴BH=$\frac{10b}{10+b}$,
∴AH=AB-BH=$\frac{100}{10+b}$,
∴S=S△AFH+S△CHA
=$\frac{1}{2}$AH•GB+$\frac{1}{2}$AH•BC
=$\frac{1}{2}$AH(GB+BC)
=$\frac{1}{2}$AH•GC
=$\frac{1}{2}$×$\frac{100}{10+b}$×(10+b)
=50
∴S的值不会发生改变;
点评 本题考查图形的面积计算,涉及三角形面积公式,正方形面积公式,完全平方公式,相似三角形的性质与判定,题目较为综合.

练习册系列答案
相关题目
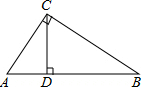 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D. 如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数.
如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数.