题目内容
18. 如图,已知AD=4,CD=3,AD⊥DC,AB=13,BC=12,求这个四边形的面积.
如图,已知AD=4,CD=3,AD⊥DC,AB=13,BC=12,求这个四边形的面积.
分析 首先根据勾股定理得出AC的长,再利用勾股定理定理得出△BAC是直角三角形,结合四边形ABCD的面积=S△ABC-S△DAC求出即可.
解答  解:连接AC,
解:连接AC,
∵∠ADC=90°,AD=4,CD=3,
∴AC=5,
∵AB=13,BC=12,
∴AC2+BC2=AB2,
∴△BAC是直角三角形,
∴S△BAC=$\frac{1}{2}$×AC×BC=$\frac{1}{2}$×5×12=30,
∴四边形ABCD的面积为:S△ABC-S△DAC=30-$\frac{1}{2}$×3×4=24.
点评 此题主要考查了勾股定理以及勾股定理的逆定理,得出△BAC是直角三角形是解题关键.

练习册系列答案
相关题目
9.已知a,b是一元二次方程x2+2x-9=0的两根,则a2+a-b的值等于( )
| A. | 7 | B. | 11 | C. | -7 | D. | -11 |
10.以下各图中,能确定∠1=∠2的是( )
| A. |  | B. |  | C. |  | D. |  |
7.一次函数y=kx-k的图象大致为( )
| A. |  | B. |  | C. |  | D. |  |
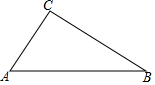 如图,Rt△ABC中,∠C=Rt∠,AC=6,BC=8,点D在BC上,D到AB的距离等于CD.
如图,Rt△ABC中,∠C=Rt∠,AC=6,BC=8,点D在BC上,D到AB的距离等于CD.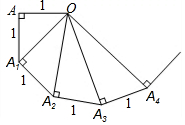 课本中有这样一句话:“利用勾股定理可以作出$\sqrt{3}$,$\sqrt{5}$,…线段(如图所示).”即:OA=1,过A作AA1⊥OA且AA1=1,根据勾股定理,得OA1=$\sqrt{2}$;再过A1作A1A2⊥OA1且A1A2=1,得OA2=$\sqrt{3}$;…以此类推,得OA2017=$\sqrt{2018}$.
课本中有这样一句话:“利用勾股定理可以作出$\sqrt{3}$,$\sqrt{5}$,…线段(如图所示).”即:OA=1,过A作AA1⊥OA且AA1=1,根据勾股定理,得OA1=$\sqrt{2}$;再过A1作A1A2⊥OA1且A1A2=1,得OA2=$\sqrt{3}$;…以此类推,得OA2017=$\sqrt{2018}$.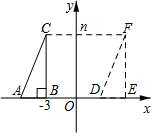 如图,直角三角形的顶点A、B在x轴上,∠ABC=90°,BC∥y轴,且C点在第二象限,B点为(-3,0),将直角三角形ABC沿x轴水平向右平移m个单位,得到对应的直角三角形DEF,其中点A、B、C分别对应点D、E、F,求:
如图,直角三角形的顶点A、B在x轴上,∠ABC=90°,BC∥y轴,且C点在第二象限,B点为(-3,0),将直角三角形ABC沿x轴水平向右平移m个单位,得到对应的直角三角形DEF,其中点A、B、C分别对应点D、E、F,求: