题目内容
 如图,AB是⊙O的直径,C是圆上一点,过点C作CD⊥AB于点D,延长CD交圆于点E,过点C作AE的平行线交圆于点F,连接EF,交AB于H,AC,EF的延长线相较于G
如图,AB是⊙O的直径,C是圆上一点,过点C作CD⊥AB于点D,延长CD交圆于点E,过点C作AE的平行线交圆于点F,连接EF,交AB于H,AC,EF的延长线相较于G(1)求证:HE2=HF•HG;
(2)HE=4,GF=
| 7 |
| 3 |
考点:相似三角形的判定与性质,圆周角定理
专题:
分析:(1)首先连接CH、CF,由四边形AEFC是圆内接四边形,过点C作AE的平行线交圆于点F,易证得∠AEF=∠CAE,继而证得∠2=∠G,即可证得△HCF∽△HGC,然后由相似三角形的对应边成比例,证得HE2=HF•HG;
(2)由HE2=HF•HG,可得EH2=HF(HF+FG),即可求得答案.
(2)由HE2=HF•HG,可得EH2=HF(HF+FG),即可求得答案.
解答: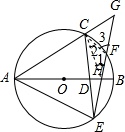 (1)证明:连接CH、CF,
(1)证明:连接CH、CF,
∵四边形AEFC是圆内接四边形,
∴∠3=∠AEF,
∵CF∥AE,
∴∠3=∠CAE,
∴∠AEF=∠CAE,
∴∠G=180°-2∠CAE,
∵∠2=180°-∠3-∠ACH,∠ACH=∠CAE=∠3,
∴∠2=∠G,
∵∠1=∠1,
∴△HCF∽△HGC,
∴CH:HG=HF:CH,
∴CH2=HF•HG,
∵CH=EH,
∴EH2=HF•HG,
(2)∵EH2=HF•HG,
∴EH2=HF(HF+FG),
∵HE=4,GF=
,
∴3HF2+7HF-48=0,
∴FH=3.
 (1)证明:连接CH、CF,
(1)证明:连接CH、CF,∵四边形AEFC是圆内接四边形,
∴∠3=∠AEF,
∵CF∥AE,
∴∠3=∠CAE,
∴∠AEF=∠CAE,
∴∠G=180°-2∠CAE,
∵∠2=180°-∠3-∠ACH,∠ACH=∠CAE=∠3,
∴∠2=∠G,
∵∠1=∠1,
∴△HCF∽△HGC,
∴CH:HG=HF:CH,
∴CH2=HF•HG,
∵CH=EH,
∴EH2=HF•HG,
(2)∵EH2=HF•HG,
∴EH2=HF(HF+FG),
∵HE=4,GF=
| 7 |
| 3 |
∴3HF2+7HF-48=0,
∴FH=3.
点评:此题考查了相似三角形的判定与性质、圆周角定理以及圆的内接四边形的性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
体育文化用品商店购进篮球和排球共7个,进价和售价如表,全部销售完后共获利润85元.则所有购进篮球和排球售价的众数、中位数是( )
| 篮球 | 排球 | |
| 进价(元/个) | 80 | 50 |
| 售价(元/个) | 95 | 60 |
| A、60,60 |
| B、60,95 |
| C、50,80 |
| D、50,50 |
“十•一五”期间,安徽省各类项目验收补充耕地100余万亩,整理过的土地亩均增产约一成,新增粮食生产能力约1.6亿斤,1.6亿用科学记数法表示为( )
| A、1.6×108 |
| B、1.6×109 |
| C、16×107 |
| D、16×108 |
 如图,在四边形ABCD中,E,F,M,N分别为AB,CD,BD,AC的中点,
如图,在四边形ABCD中,E,F,M,N分别为AB,CD,BD,AC的中点,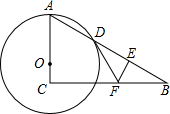 如图,已知点O是Rt△ABC的直角边AC上的一动点,以O为圆心,OA为半径的⊙O交AB于D点,DB垂直平分线交BC于F,交BD于E.
如图,已知点O是Rt△ABC的直角边AC上的一动点,以O为圆心,OA为半径的⊙O交AB于D点,DB垂直平分线交BC于F,交BD于E. 如图,已知两棵小树在同一时刻的影子,请画出此时的光线,并指出影子是在什么光线下形成的?
如图,已知两棵小树在同一时刻的影子,请画出此时的光线,并指出影子是在什么光线下形成的? 如图,以O为顶点的角有
如图,以O为顶点的角有 某校的校园内有一个由两个相同的正六边形(边长为2.5m)围成的花坛,如图中的阴影部分所示,校方先要将这个花坛在原有的基础上扩建成一个菱形区域如图所示,并在新扩充的部分种上草坪,则扩建后菱形区域的周长为( )
某校的校园内有一个由两个相同的正六边形(边长为2.5m)围成的花坛,如图中的阴影部分所示,校方先要将这个花坛在原有的基础上扩建成一个菱形区域如图所示,并在新扩充的部分种上草坪,则扩建后菱形区域的周长为( )